如图,在矩形ABCD中,AC与BD相交于O,∠COD=60°,点E是BC边上的动点,连结DE,OE.
(1)求证:△COD是等边三角形;
(2)如图1,当DE平分∠ADC时,试证明OC=EC,并求出∠DOE的度数;
(3)如图2,当DE平分∠BDC时,试证明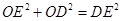 .
.
已知关于x的函数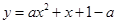 (a为常数)
(a为常数)
(1)若函数的图象与坐标轴恰有两个交点,求a的值;
(2)若函数的图象是抛物线,开口向上且顶点在x轴下方,求a的取值范围.
如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.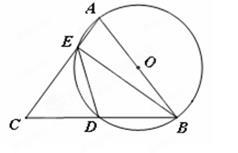
(1)试判断DE与BD是否相等,并说明理由;
(2)如果BC=6,AB=5,求BE的长.
甲口袋中装有3个相同的小球,它们分别写有数值﹣1,2,5;乙口袋中装有3个相同的小球,它们分别写有数值﹣4,2,3.现从甲口袋中随机取一球,记它上面的数值为x,再从乙口袋中随机取一球,记它上面的数值为y.设点A的坐标为(x,y).
(1)请用树状图或列表法表示点A的坐标的各种可能情况;
(2)求点A落在 的概率.
的概率.
如图,在⊿ABC中,AB=BC,点D在AB的延长线上。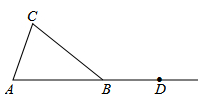
(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)①作∠CBD的平分线BM ②作边BC上的中线AE,并延长AE交BM于点F.
(2)在(1)的基础上,连接CF,判断四边形ABFC的形状,并说明理由。
先化简,再求值: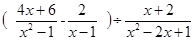 ,其中
,其中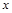 是不等式组
是不等式组 的整数解。
的整数解。