某校师生到距学校20千米的公路旁植树,甲班师生骑自行车先走,45分钟后,乙班师生乘汽车出发,结果两班师生同时到达,已知汽车的速度是自行车速度的2.5倍,求两种车的速度各是多少?
某校在周二至周四的课余时间分别开设了“国学”、“拉丁舞”、“机器人”三门选修课课程.
(1)若小莹任意选修其中两门课程,求选修两门课程中含有国学的概率?
(2)若小莹和小亮各自任意选修一门课程,求两人选修同一门课程的概率?
已知反比例函数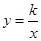 的图象与一次函数
的图象与一次函数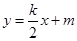 的图象交点为(2,2).
的图象交点为(2,2).
(1)求这两个函数的解析式;
(2)在下面的坐标纸中大致画出两个函数的图象,根据图象写出不等式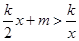 的解集.
的解集.
如图所示的粮仓可以看成圆柱体与圆锥体的组合体,已知其底面半径为6米,高为4米,下方圆柱高为3米.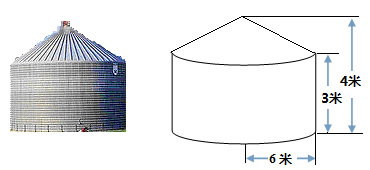
(1)求该粮仓的容积;
(2)求上方圆锥的侧面积.(计算结果保留根号)
如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.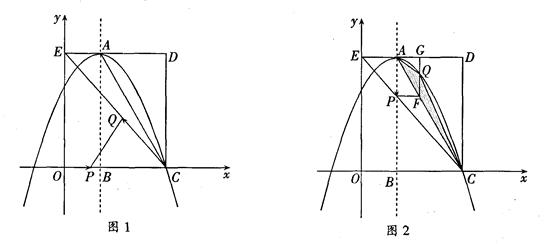
(1)填空:点A坐标为,抛物线的解析式为;
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.连接PQ,是否存在实数t,使得PQ所在的直线经过点D,若存在,求出t的值;若不存在,请说明理由;
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
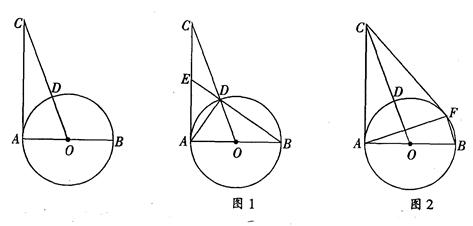
如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D.
(1)如图1,连接BD并延长BD交AC于点E,连接AD.
①证明:△CDE∽△CAD;
②若AB=2,AC=2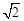 .求CD和CE的长;
.求CD和CE的长;
(2)如图2,过点C作⊙O的另一条切线,切点为F,连结AF、BF,若OC= BF,求
BF,求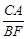 的值.
的值.