(本题满分12分)已知正方体ABCD-A1B1C1D1,求证:平面AB1D1∥平面C1BD.
如图,在四棱锥 中,底面
中,底面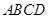 是边长为
是边长为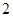 的正方形,侧面
的正方形,侧面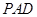
 底面
底面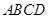 ,且
,且 ,
,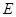 、
、 分别为
分别为 、
、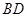 的中点.
的中点.
(Ⅰ)求证: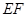 //平面
//平面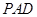 ;
;
(Ⅱ)求证:平面
 平面
平面 ;
;
(Ⅲ)在线段 上是否存在点
上是否存在点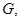 使得二面角
使得二面角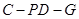 的余弦值为
的余弦值为 ?若存在,求
?若存在,求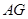 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
在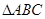 中,
中,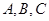 的对边分别为
的对边分别为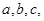 且
且 成等差数列.
成等差数列.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的范围.
的范围.
一个袋子中装有大小形状完全相同的编号分别为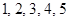 的
的 个红球与编号为
个红球与编号为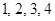 的
的 个白球,从中任意取出
个白球,从中任意取出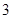 个球.
个球.
(Ⅰ)求取出的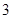 个球颜色相同且编号是三个连续整数的概率;
个球颜色相同且编号是三个连续整数的概率;
(Ⅱ)记 为取出的
为取出的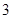 个球中编号的最大值,求
个球中编号的最大值,求 的分布列与数学期望.
的分布列与数学期望.
已知函数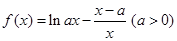
(Ⅰ)求函数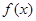 的单调区间与极值;
的单调区间与极值;
(Ⅱ)求证:对于任意正整数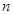 ,均有
,均有 (
( 为自然对数的底数);
为自然对数的底数);
(Ⅲ)当 时,是否存在过点
时,是否存在过点 的直线与函数
的直线与函数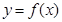 的图象相切?若存在,有多少条?若不存在,说明理由.
的图象相切?若存在,有多少条?若不存在,说明理由.
设数列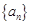 的前
的前 项和为
项和为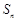 .已知
.已知 ,
,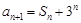 ,
,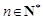 .
.
(Ⅰ)设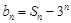 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)若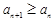 ,
,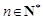 ,求
,求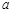 的取值范围.
的取值范围.