已知三个不等式x2-4x+3<0…①,x2-6x+8<0…②,2x2-9x+m<0…③,要使同时满足①和②的所有x的值都满足③,则实数m的取值范围是( )
| A.m>9 | B.m=9 | C.m≤9 | D.0<m≤9 |
在实数集 中,我们定义的大小关系“
中,我们定义的大小关系“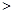 ”为全体实数排了一个“序”,类似地,我们在复数集
”为全体实数排了一个“序”,类似地,我们在复数集 上也可以定义一个称为“序”的关系,记为“
上也可以定义一个称为“序”的关系,记为“ ”。定义如下:对于任意两个复数
”。定义如下:对于任意两个复数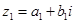 ,
,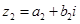 (
( ,
, 为虚数单位),“
为虚数单位),“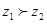 ”当且仅当“
”当且仅当“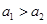 ”或“
”或“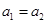 且
且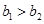 ”.下面命题为假命题的是()
”.下面命题为假命题的是()
A.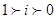 |
B.若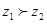 , ,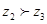 ,则 ,则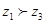 |
C.若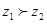 ,则对于任意 ,则对于任意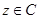 , , |
D.对于复数 ,若 ,若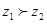 ,则 ,则 |
函数 的图象(如图),则函数
的图象(如图),则函数 的单调递增区间是()
的单调递增区间是()
A.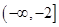 |
B. |
C.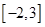 |
D.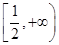 |
在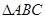 中,
中,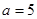 ,
,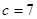 ,
, , 则三角形的面积为()
, 则三角形的面积为()
A.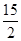 |
B. |
C.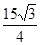 |
D.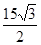 |
如图,为了得到这个函数的图象,只要将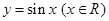 的图象上所有的点( )
的图象上所有的点( )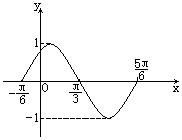
A.向左平移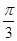 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的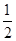 倍,纵坐标不变 倍,纵坐标不变 |
B.向左平移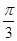 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移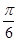 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的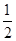 倍,纵坐标不变 倍,纵坐标不变 |
D.向左平移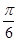 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
平面上有一个△ABC和一点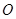 ,设
,设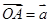 ,
,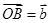 ,
,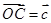 ,又
,又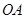 、
、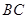 的中点分别为
的中点分别为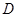 、
、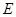 ,则向量
,则向量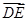 等于( )
等于( )
A.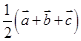 |
B.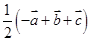 |
C.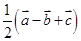 |
D.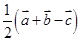 |