阅读理解填空:
(1)如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.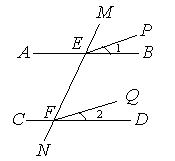
证明:∵AB∥CD,
∴∠MEB=∠MFD( )
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥_____.( )
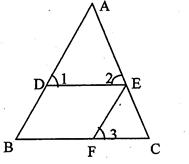
(2)如图,EF∥AD,∠1=∠2,∠BAC=70 o,求∠AGD.
解:∵EF∥AD,
∴∠2= ( )
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥ ( )
∴∠BAC+ =180 o( )
∵∠BAC=70 o,
∴∠AGD= 。
如图,∠1=∠2=∠B,EF//AB.观察猜想:∠3和∠C有什么数量关系?
对观察猜想的结论给出证明.
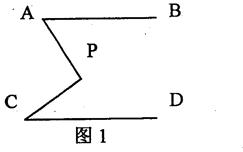
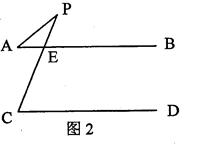
分别探讨下面两个图形中∠APC与∠A、∠C的数量关系;
请你从所得到的关系中任选一个加以证明.
如图,在平面直角坐标系中,已知三个点A(1,3),B(3,1),O(0,0).求△ABO的面积;
将△ABO向左平移4个单位长度,向下平移1个单位长度,得到△DEF,其中A,B,O分
别对应点D,E,F,请在图中画出△DEF,并写出D、E、F的坐标.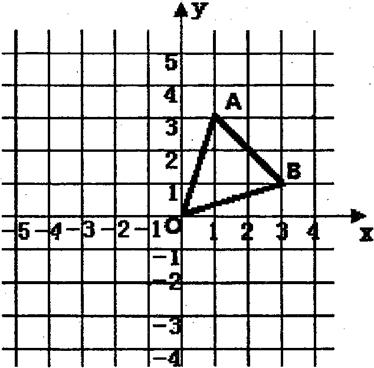
如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=43°,∠C=77°,求∠BAE和∠DAE的度数.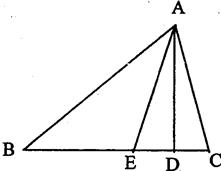
甲、乙两人相距35km,若两人相向而行,2小时后两人相遇;若两人同向而行,5小时后甲追上乙,求甲、乙两人的速度.