(本小题满分12分)
已知函数 (
( ),
),
(Ⅰ)求函数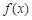 的最小值;
的最小值;
(Ⅱ)已知 ,
, :关于
:关于 的不等式
的不等式 对任意
对任意 恒成立;
恒成立; :函数
:函数 是增函数.若“
是增函数.若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
已知数列 满足:
满足: ,
,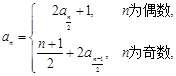 ,
,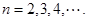
(Ⅰ)求 的值;
的值;
(Ⅱ)设 ,试求数列
,试求数列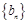 的通项公式;
的通项公式;
(Ⅲ)对于任意的正整数n,试讨论并证明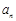 与
与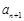 的大小关系.
的大小关系.
已知函数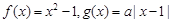 .
.
(Ⅰ)若当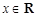 时,不等式
时,不等式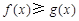 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅱ)求函数 在区间
在区间 上的最大值.
上的最大值.
平面直角坐标系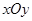 中,过椭圆
中,过椭圆 右焦点的直线
右焦点的直线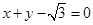 交
交 于
于 两点,
两点, 为
为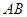 的中点,且
的中点,且 的斜率为
的斜率为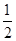 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)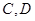 为
为 上的两点,若四边形
上的两点,若四边形 的对角线
的对角线 ,求四边形ACBD面积的最大值.
,求四边形ACBD面积的最大值.
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.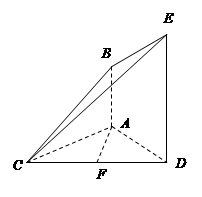
(Ⅰ)求证:平面CBE⊥平面CDE;
(Ⅱ)求二面角C—BE—F的余弦值.
在 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 .
.
(Ⅰ)求角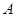 的大小;
的大小;
(Ⅱ)若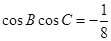 ,且
,且 的面积为
的面积为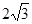 ,求
,求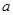 .
.