甲、乙两地相距s km , 汽车从甲地匀速行驶到乙地,速度不得超过c km/h ,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(km/h)的平方成正比,比例系数为b;固定部分为a元。把全程运输成本y(元)表示为速度v(km/h)的函数,并指出这个函数的定义域;为了使全程运输成本最小,汽车应以多大速度行驶?
在数列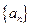 中,
中,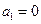 ,且对任意
,且对任意 .
.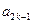 ,
,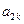 ,
, 成等差数列,其公差为
成等差数列,其公差为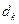 。
。
(Ⅰ)若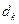 =
= ,证明
,证明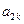 ,
, ,
,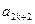 成等比数列(
成等比数列( )
)
(Ⅱ)若对任意 ,
,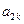 ,
, ,
,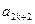 成等比数列,其公比为
成等比数列,其公比为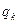 。
。
如图,在长方体 中,
中,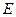 、
、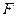 分别是棱
分别是棱 ,
,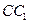
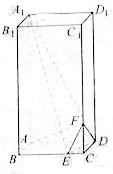
上的点,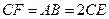 ,
,
(1)求异面直线 与
与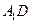 所成角的余弦值;
所成角的余弦值;
(2)证明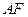
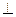 平面
平面
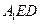
(3)求二面角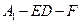 的正弦值。
的正弦值。
已知函数
(Ⅰ)求函数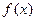 的最小正周期及在区间
的最小正周期及在区间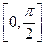 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若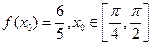 ,求
,求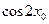 的值。
的值。
已知函数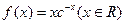
(Ⅰ)求函数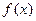 的单调区间和极值;
的单调区间和极值;
(Ⅱ)已知函数 的图象与函数
的图象与函数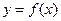 的图象关于直线
的图象关于直线 对称,证明当
对称,证明当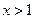 时,
时,
(Ⅲ)如果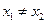 ,且
,且 ,证明
,证明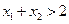
已知椭圆 的离心率
的离心率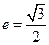 ,连接椭圆的四个顶点得到的菱形的面积为4。
,连接椭圆的四个顶点得到的菱形的面积为4。
(1)求椭圆的方程;
(2)设直线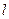 与椭圆相交于不同的两点
与椭圆相交于不同的两点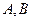 ,已知点
,已知点 的坐标为(
的坐标为(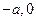 ),点
),点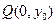 在线段
在线段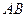 的垂直平分线上,且
的垂直平分线上,且 ,求
,求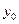 的值
的值