(本小题满分14分)
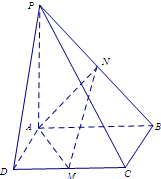
如图4,已知四棱锥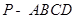 ,底面
,底面 是正方形,
是正方形,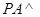 面
面 ,点
,点 是
是 的中点,点
的中点,点 是
是 的中点,连接
的中点,连接 ,
,
 .
.
(1)求证: 面
面 ;
;
(2)若 ,
,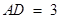 ,求二面角
,求二面角 的余弦值.
的余弦值.
设m,n是给定的整数,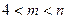 ,
,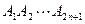 是一个正2n+1边形,
是一个正2n+1边形,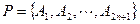 .求顶点属于P且恰有两个内角是锐角的凸m边形的个数.
.求顶点属于P且恰有两个内角是锐角的凸m边形的个数.
求所有的素数对(p,q),使得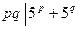 .
.
给定锐角三角形PBC,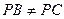 .设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.(1)若A,B,C,D四点共圆,求证:
.设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.(1)若A,B,C,D四点共圆,求证: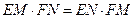 ;
;
(2)若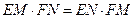 ,是否一定有A,B,C,D四点共圆?证明你的结论.
,是否一定有A,B,C,D四点共圆?证明你的结论.
某家具厂有方木料90m3,五合板60㎡,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1 m3、五合板2㎡,生产每个书橱需要方木料0.2 m3、五合板1㎡,出售一张书桌可获得利润80元,出售一个书橱可获得利润120元.如果只安排生产书桌,可获利润多少?如果只安排生产书橱,可获利润多少?怎样安排生产可使所得利润最大?
某人有楼房一幢,室内面积共180㎡,拟分隔两类房间作为旅游客房.大每间面积为18㎡,可住游客5名,每名游客每天住宿费为40元;小房间每间面积为15㎡,可住游客3名,每名游客每天住宿费为50元;装修大房间每间需1000元,装修小房间每间需600元.如果他只能筹款8000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,能获得最大收益?