(本小题满分13分).某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为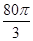 立方米,且
立方米,且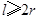 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.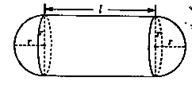
(Ⅰ)写出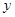 关于
关于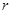 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的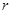 .
.
(本小题满分12分)
已知函数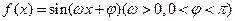 的一系列对应值如表:
的一系列对应值如表:
 |
… |
 |
0 |
 |
 |
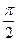 |
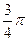 |
… |
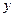 |
… |
0 |
1 |
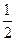 |
0 |
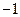 |
0 |
… |
(1)求 的解析式;
的解析式;
(2)若在△ABC中,AC=2,BC=3,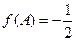 (A为锐角),求△ABC的面积。
(A为锐角),求△ABC的面积。
已知函数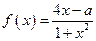 在区间
在区间 上为增函数,且
上为增函数,且 。
。
(1)当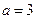 时,求
时,求 的值;
的值;
(2)当 最小时,
最小时,
①求 的值;
的值;
②若 是
是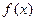 图象上的两点,且存在实数
图象上的两点,且存在实数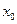 使得
使得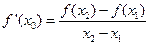 ,证明:
,证明: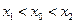 。
。
.如图, ,过曲线
,过曲线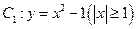 上一点
上一点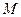 的切线
的切线 ,与曲线
,与曲线 也相切于点
也相切于点 ,记点
,记点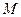 的横坐标为
的横坐标为 。
。
(1)用 表示
表示 的值和点
的值和点 的坐标;
的坐标;
(2)当实数 取何值时,
取何值时,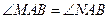 ?
?
并求此时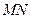 所在直线的方程。
所在直线的方程。
如图,在矩形 中,
中,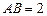 ,
,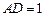 ,
,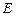 是
是 的中点,以
的中点,以 为折
为折 痕将
痕将 向上折起,使
向上折起,使 为
为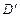 ,且平面
,且平面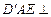 平面
平面
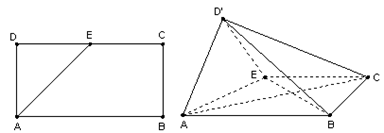
(Ⅰ)求证: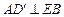 ;
;
(Ⅱ)求二面角 的大小
的大小
.在1,2,3,4,5的所有排列 中,
中,
(1)求满足 的概率;
的概率;
(2)记 为某一排列中满足
为某一排列中满足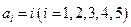 的个数,求
的个数,求 的分布列和数学期望。
的分布列和数学期望。