某班从6名班干部(其中男生4人,女生2人)中,任选3人参加学校的
义务劳动.
(1) 求男生甲或女生乙被选中的概率
(2)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B)和P(A|B).
已知正项数列 满足:
满足:
(1)求 的范围,使得
的范围,使得 恒成立;
恒成立;
(2)若 ,证明:
,证明:
已知函数 (其中a,b为常数且
(其中a,b为常数且 )的反函数的图象经过点A(4,1)和B(16,3).
)的反函数的图象经过点A(4,1)和B(16,3).
(1)求a,b的值;
(2)若不等式 在
在 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.
如图,已知离心率为 的椭圆
的椭圆 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线 交椭圆C于不同的两点A、B.
交椭圆C于不同的两点A、B.
(1)求椭圆C的方程.
(2)证明:直线MA、MB与x轴围成一个等腰三角形.
如图,在直三棱柱 中,
中,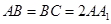 ,
, ,
, 是
是 的中点.
的中点.
(1)求证: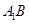 ∥平面
∥平面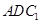 ;
;
(2)求二面角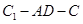 的余弦值;
的余弦值;
(3)试问线段 上是否存在点
上是否存在点 ,使
,使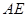 与
与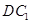 成
成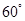 角?若存在,确定
角?若存在,确定 点位置,若不存在,说明理由.
点位置,若不存在,说明理由. 