已知椭圆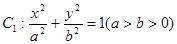 经过点
经过点 ,且其右焦点与抛物线
,且其右焦点与抛物线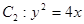 的焦点F重合.
的焦点F重合.
(Ⅰ)求椭圆 的方程;
的方程;
(II)直线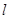 经过点
经过点 与椭圆
与椭圆 相交于A、B两点,与抛物线
相交于A、B两点,与抛物线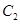 相交于C、D两点.求
相交于C、D两点.求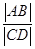 的最大值.
的最大值.
已知函数
(1)求函数
的单调区间;
(2)若函数
的图像与直线
恰有两个交点,求
的取值范围.
如图,正三棱锥 的三条侧棱 两两垂直,且长度均为2. 分别是 的中点, 是 的中点,过 的平面与侧棱 或其延长线分别相交于 ,已知 .
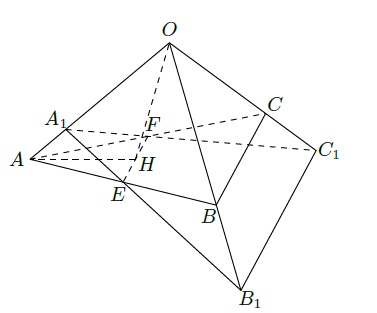
(1)求证:
⊥面
;
(2)求二面角
的大小.
等差数列
的各项均为正数,
,前
项和为
,
为等比数列,
,且
,
.
(1)求
与
;
(2)求和: .
因冰雪灾害,某柑桔基地果林严重受损,为此有关专家提出一种拯救果树的方案,该方案需分两年实施且相互独立.该方案预计第一年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.2、0.4、0.4;第二年可以使柑桔产量为第一年产量的1.5倍、1.25倍、1.0倍的概率分别是0.3、0.3、0.4.
(1)求两年后柑桔产量恰好达到灾前产量的概率;
(2)求两年后柑桔产量超过灾前产量的概率.
已知 , ,
(1)求
的值;
(2)求函数
的最大值.