(本题10分)双曲线的离心率等于4,且与椭圆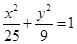 有相同的焦点,求此双曲线方程.
有相同的焦点,求此双曲线方程.
已知数列{an}各项均为正数,其前n项和为Sn,且满足4Sn=(an+1)2.[来
(1)求{an}的通项公式;(2)设bn=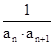 ,数列{bn}的前n项和为Tn,求Tn的最小值.
,数列{bn}的前n项和为Tn,求Tn的最小值.
已知函数f(x)=msinx+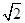 cosx(m>0)的最大值为2.
cosx(m>0)的最大值为2.
(1)求函数f(x)在[0,π]上的单调递减区间;(2)△ABC中,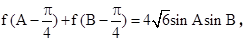 角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.
角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.
已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N*,数列{bn}满足an=4log2bn+3,n∈N*.
(1)求an,bn; (2)求数列{an·bn}的前n项和Tn.
已知函数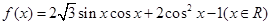 ,
,
(1)求函数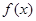 的最小正周期及在区间
的最小正周期及在区间 上的最大值和最小值;
上的最大值和最小值;
(2)若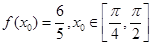 ,求
,求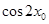 的值.
的值.
已知函数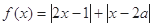 .
.
(1)当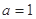 时,求
时,求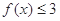 的解集;
的解集;
(2)当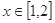 时,
时,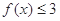 恒成立,求实数
恒成立,求实数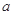 的集合.
的集合.