(本小题12分)
四棱锥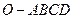 中,
中, 底面
底面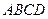 ,且
,且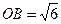 ,底面
,底面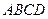 是菱形;点
是菱形;点 在平面
在平面 内的射影
内的射影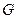 恰为
恰为 的重心.
的重心.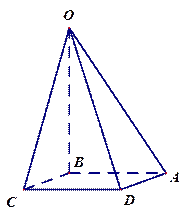 ①求
①求 的长;
的长;
②求二面角 的平面角的余弦值.
的平面角的余弦值.
(本小题满分l2分)(注意:在试题卷上作答无效)
在 ABC中,C-A=
ABC中,C-A=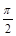 , sinB=
, sinB= 。
。
(I)求sinA的值;
(II)设AC=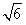 ,求
,求 ABC的面积。
ABC的面积。
(本小题满分l2分)(注意:在试题卷上作答无效)
已知 的三个顶点的坐标为
的三个顶点的坐标为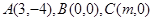
(I)若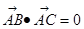 ,求
,求 的值;
的值;
(II)若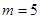 ,求
,求 的值.
的值.
(本小题满分l0分)(注意:在试题卷上作答无效)
设递增等差数列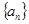 的前
的前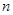 项和为
项和为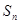 ,已知
,已知 ,
, 是
是 和
和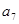 的等比中项,
的等比中项,
(I)求数列 的通项公式;
的通项公式;
(II)求数列 的前
的前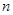 项和
项和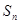 .
.
(本小题满分10分)选修4—5:不等式选讲
已知函数 (Ⅰ)求不等式
(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若关于x的不等式 的解集非空,求实数
的解集非空,求实数 的取值范围.
的取值范围.
(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系中,以原点为极点, 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线
 ,已知过点
,已知过点 的直线
的直线 的参数方程为:
的参数方程为: ,
,
直线 与曲线
与曲线 分别交于
分别交于 .
.
(Ⅰ)写出曲线 和直线
和直线 的普通方程;(Ⅱ)若
的普通方程;(Ⅱ)若 成等比数列,求
成等比数列,求 的值.
的值.