函数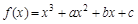 ,过曲线
,过曲线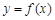 上的点
上的点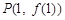 的切线方程为
的切线方程为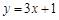
(Ⅰ)若 在
在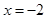 时有极值,求
时有极值,求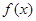 的表达式;
的表达式;
(Ⅱ)若函数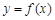 在区间
在区间 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.
已知函数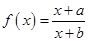 (
(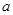 、
、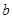 为常数).
为常数).
(1)若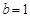 ,解不等式
,解不等式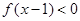 ;
;
(2)若 ,当
,当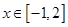 时,
时,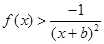 恒成立,求
恒成立,求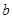 的取值范围.
的取值范围.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.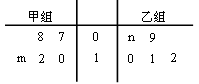
(1)求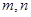 的值;
的值;
(2)分别求出甲、乙两组数据的方差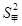 和
和 ,
,
并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件数之和大于17,则称该车间“质量合格”,求该车间“质量合格”的概率.
(注:方差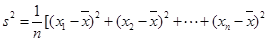 ,
, 为数据
为数据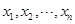 的平均数)
的平均数)
在 中,角
中,角 对的边分别为
对的边分别为 ,且
,且 .
.
(1)求 的值;
的值;
(2)若 ,求
,求 的面积
的面积 .
.
在等比数列 中,
中, ,且
,且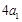 ,
, ,
, 成等差数列.
成等差数列.
(1)求 ;
;
(2)令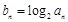 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知点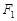 、
、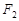 为双曲线
为双曲线 :
:
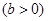 的左、右焦点,过
的左、右焦点,过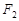 作垂直于
作垂直于 轴的直线,在
轴的直线,在 轴上方交双曲线
轴上方交双曲线 于点
于点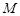 ,且
,且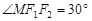 ,圆
,圆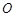 的方程是
的方程是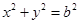 .
.
(1)求双曲线 的方程;
的方程;
(2)过双曲线 上任意一点
上任意一点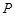 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为 、
、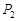 ,求
,求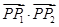 的值;
的值;
(3)过圆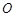 上任意一点
上任意一点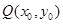 作圆
作圆 的切线
的切线 交双曲线
交双曲线 于
于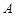 、
、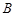 两点,
两点,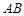 中点为
中点为 ,求证:
,求证: .
.