(本小题满分13分)
已知数列{an}的首项a1=" t" >0, ,n=1,2,……
,n=1,2,……
(1)若t =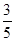 ,求
,求 是等比数列,并求出{an}的通项公式;
是等比数列,并求出{an}的通项公式;
(2)若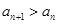 对一切
对一切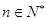 都成立,求t的取值范围.
都成立,求t的取值范围.
已知函数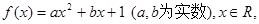
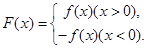
(1)若不等式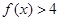 的解集为
的解集为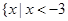 或
或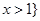 ,求
,求 的表达式;
的表达式;
(2)在(1)的条件下, 当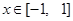 时,
时, 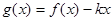 是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;
(3)设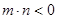 ,
, 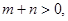
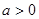 且
且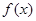 为偶函数, 判断
为偶函数, 判断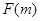 +
+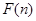 能否大于零?
能否大于零?
设函数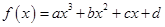 (a>0),且方程
(a>0),且方程 (x)-9x=0的两个根分别为1,4.
(x)-9x=0的两个根分别为1,4.
(1)当a=3且曲线y="f" (x)过原点时,求f (x)的解析式;
(2)若f (x)在(-∞,+∞)内无极值点,求a的取值范围.
){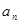 }、{
}、{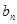 }都是各项为正的数列,对任意的
}都是各项为正的数列,对任意的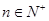 ,都有
,都有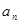 、
、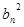 、
、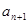 成等差数列,
成等差数列,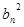 、
、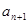 、
、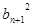 成等比数列.
成等比数列.
(1) 试问{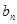 }是否为等差数列,为什么?
}是否为等差数列,为什么?
(2) 如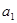 =1,
=1,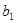 =
=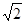 ,求
,求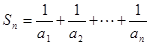 ;
;
已知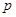 :
: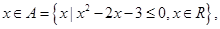
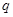 :
: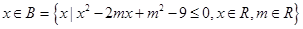
(1)若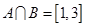 ,求实数
,求实数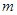 的值;
的值;
(2)若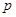 是
是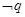 的充分条件,求实数
的充分条件,求实数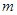 的取值范围.
的取值范围.
已知 为等差数列,
为等差数列,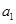 +
+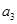 +
+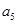 =105,
=105,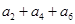 =99,
=99,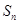 表示
表示 的前
的前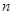 项和,问n取什么值
项和,问n取什么值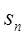 最大。
最大。