“水是生命之源”，市自来水公司为鼓励用户节约用水，按以下规定收取水费：
| 用水量/月 |
单价(元/吨) |
| 不超过20吨的部分 |
2.2 |
| 超过20吨的部分 |
2.7 |
(1)某用户1月份共交水费71元，问1月份该用户用水多少吨？
(2)若该用户水表有故障，每次用水只有60%记入用水量，这样2月份共交水费33元，该用户2月份实际应交水费多少元？
.如图，在直角坐标系中，点A是反比例函数y1=
的图象上一点，AB⊥x轴的正半轴于点B，C是OB的中点，一次函数y2=ax+b的图象经过A、C两点，并交y轴于点D(0,－2)，若S△AO D=4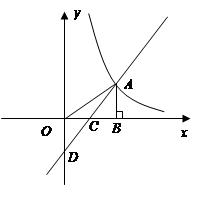
（1）求反比例函数和一次函数解析式。
（2）观察图象，请指出在y轴的右侧，当y1＞y2时x 的取值范围
“中华人民共和国道路交通管理条例”规定：小汽车在城市街路上行驶的速度不得超过70千米/时，一辆小汽车在一条城市街路的直道上行驶，某一时刻刚好行驶在路边车速检测仪的北偏东30°距离30米处，过了2秒后行驶了50米，此时测得小汽车与车速检测仪间的距离为40米. 问：2秒后小汽车在车速检测仪的哪个方向?这辆小汽车超速了吗?
解方程：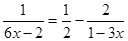
先化简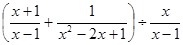
，然后选取一个你喜欢的
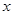的值代入计算.
已知：如图1，线段AB、CD相交于点O，连结AD、CB，我们把形如图1的图形称之为“8字形”．试解答下列问题：
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：________________________；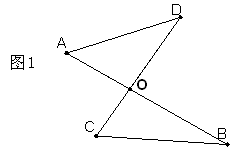
（2）仔细观察，在图2中“8字形”的个数：__________个；
（3）在图2中，若∠D=40°,∠B=36°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．利用（１）的结论，试求∠P的度数；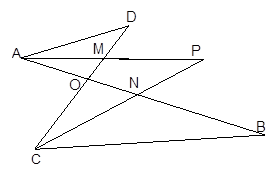
|