在一条笔直的河道上依次有A、B、C三个港口，甲、乙两船同时分别从A、B 港口出发，沿直线匀速驶向C港，最终到达C港．设甲、乙两船行驶x(h)后，与B港的距离分别为y1、y2(km)，y1、y2与x的函数关系如图所示(点P、Q为图象的交点)．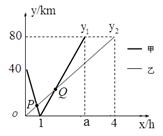
（1）填空：A、C两港口间的距离为 km，a＝ ；
（2）求y1与x的函数关系式，并写出自变量x的取值范围；
（3）求图中点P的坐标，并解释该点坐标所表示的实际意义。
（贵港）如图，已知AB是⊙O的弦，CD是⊙O的直径，CD⊥AB，垂足为E，且点E是OD的中点，⊙O的切线BM与AO的延长线相交于点M，连接AC，CM．
（1）若AB=
，求
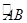的长；（结果保留π）
（2）求证：四边形ABMC是菱形．
（贵港）如图，一次函数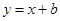
的图象与反比例函数
的图象交于点A和点B（﹣2，n），与x轴交于点C（﹣1，0），连接OA．
（1）求一次函数和反比例函数的解析式；
（2）若点P在坐标轴上，且满足PA=OA，求点P的坐标．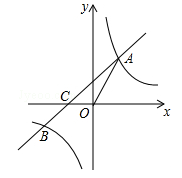
（崇左）如图，在平面直角坐标系中，点M的坐标是（5，4），⊙M与y轴相切于点C，与x轴相交于A、B两点．
（1）则点A、B、C的坐标分别是A（__，__），B（__，__），C（__，__）；
（2）设经过A、B两点的抛物线解析式为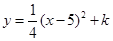
，它的顶点为F，求证：直线FA与⊙M相切；
（3）在抛物线的对称轴上，是否存在点P，且点P在x轴的上方，使△PBC是等腰三角形．如果存在，请求出点P的坐标；如果不存在，请说明理由．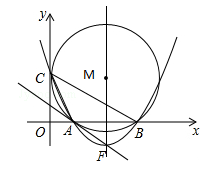
（崇左）一块材料的形状是锐角三角形ABC，边BC=120mm，高AD=80mm，把它加工成正方形零件如图1，使正方形的一边在BC上，其余两个顶点分别在AB、AC上．
（1）求证：△AEF∽△ABC；
（2）求这个正方形零件的边长；
（3）如果把它加工成矩形零件如图2，问这个矩形的最大面积是多少？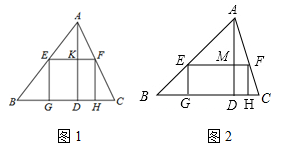
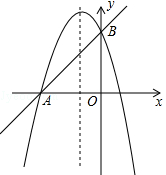
（贺州）如图，已知抛物线
与直线AB相交于A（﹣3，0），B（0，3）两点．
（1）求这条抛物线的解析式；
（2）设C是抛物线对称轴上的一动点，求使∠CBA=90°的点C的坐标；
（3）探究在抛物线上是否存在点P，使得△APB的面积等于3？若存在，求出点P的坐标；若不存在，请说明理由．