(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知函数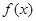 =
=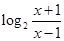 .
.
(1)判断函数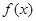 的奇偶性,并证明;
的奇偶性,并证明;
(2)求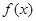 的反函数
的反函数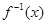 ,并求使得函数
,并求使得函数 有零点的实数
有零点的实数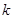 的取值范围.
的取值范围.
已知函数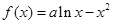 .
.
(1)当 时,求函数
时,求函数 在
在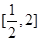 上的最大值;
上的最大值;
(2)令 ,若
,若 在区间
在区间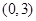 上不单调,求
上不单调,求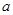 的取值范围;
的取值范围;
(3)当 时,函数
时,函数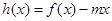 的图象与
的图象与 轴交于两点
轴交于两点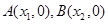 ,且
,且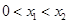 ,又
,又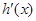 是
是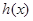 的导函数.若正常数
的导函数.若正常数 满足条件
满足条件 .证明:
.证明: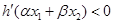 .
.
已知函数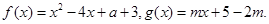
⑴当 时,若函数
时,若函数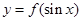 存在零点,求实数
存在零点,求实数 的取值范围并讨论零点个数;
的取值范围并讨论零点个数;
⑵当 时,若对任意的
时,若对任意的 ,总存在
,总存在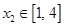 ,使
,使 成立,求实数
成立,求实数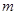 的取值范围.
的取值范围.
某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段: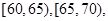
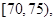

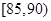 后得到如图4的频率分布直方图.
后得到如图4的频率分布直方图.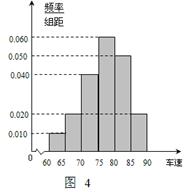
问:(1)求这40辆小型车辆车速的众数和中位数的估计值.(2)若从车速在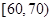 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在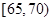 的车辆数
的车辆数 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
设等差数列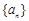 的前n项和为
的前n项和为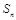 ,且
,且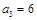 ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列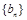 前n项和为
前n项和为 ,且
,且 ,令
,令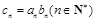 .求数列
.求数列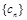 的前n项和
的前n项和 .
.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥面ABC,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且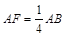 .
.
(Ⅰ)求证:EF∥平面BDC1;
(Ⅱ)求二面角E-BC1-D的余弦值.