(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
(文)某种型号汽车的四个轮胎半径相同,均为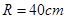 ,该车的底盘与轮胎中心在同一水平面上. 该车的涉水安全要求是:水面不能超过它的底盘高度. 如图所示:某处有一“坑形”地面,其中坑
,该车的底盘与轮胎中心在同一水平面上. 该车的涉水安全要求是:水面不能超过它的底盘高度. 如图所示:某处有一“坑形”地面,其中坑 形成顶角为
形成顶角为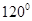 的等腰三角形,且
的等腰三角形,且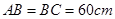 ,如果地面上有
,如果地面上有 (
(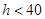 )高的积水(此时坑内全是水,其它因素忽略不计).
)高的积水(此时坑内全是水,其它因素忽略不计).
(1)当轮胎与 、
、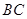 同时接触时,求证:此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为
同时接触时,求证:此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为 ;
;
(2) 假定该汽车能顺利通过这个坑(指汽车在过此坑时,符合涉水安全要求),求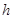 的最大值.
的最大值.
(精确到1cm).
设某物体一天中的温度T是时间t的函数,已知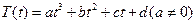 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度T关于时间t的函数关系式;
(2)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
在长为100千米的铁路线AB旁的C处有一个工厂,工厂与铁路的距离CA为20千米.由铁路上的B处向工厂提供原料,公路与铁路每吨千米的货物运价比为5∶3,为节约运费,在铁路的D处修一货物转运站,设AD距离为x千米,沿CD直线修一条公路(如图).
(1)将每吨货物运费y(元)表示成x的函数.
(2)当x为何值时运费最省?
一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
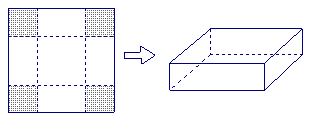
在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
 |
设工厂到铁路线的垂直距离为20km,垂足为B.铁路线上距离B为100km处有一原料供应站C,现要在铁路BC之间某处D修建一个原料中转车站,再由车站D向工厂修一条公路.如果已知每千米的铁路运费与公路运费之比为3:5,那么,D应选在何处,才能使原料供应站C运货到工厂A所需运费最省?