二次函数f(x)=px2+qx+r中实数p、q、r满足 =0,其中m>0,求证:
=0,其中m>0,求证:
(1)pf(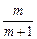 )<0;
)<0;
(2)方程f(x)=0在(0,1)内恒有解.
已知椭圆的两个焦点分别为 ,离心率
,离心率 。
。
(1)求椭圆方程;
(2)一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N,且线段MN中点的横坐标为– ,求直线l倾斜角的取值范围。
,求直线l倾斜角的取值范围。
已知抛物线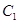 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线 :
: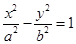 的左焦点
的左焦点 且垂直于
且垂直于 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线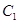 与双曲线
与双曲线 的一个交点是
的一个交点是 .
.
(1)求抛物线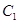 的方程及其焦点
的方程及其焦点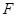 的坐标;
的坐标;
(2)求双曲线 的方程及其离心率
的方程及其离心率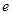 .
.
已知椭圆的两焦点是F1(0,-1),F2(0,1),离心率e=
(1)求椭圆方程;
(2)若P在椭圆上,且|PF1|-|PF2|=1,求cos∠F1PF2
在锐角 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
,
(1)求 的值;
的值;
(2)若 ,
, ,求
,求 的值.
的值.
设 是公比大于1的等比数列,
是公比大于1的等比数列, 为数列
为数列 的前
的前 项和.已知
项和.已知 ,且
,且 构成等差数列.
构成等差数列.
(1)求数列 的通项公式.
的通项公式.
(2)令 求数列
求数列 的前
的前 项和
项和 .
.