已知函数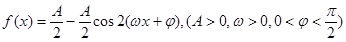 的图象过点(1,2),相邻两条对称轴间的距离为2,且
的图象过点(1,2),相邻两条对称轴间的距离为2,且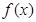 的最大值为2.
的最大值为2.
(Ⅰ)求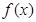 的单调递增区间;
的单调递增区间;
(Ⅱ)计算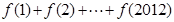 ;
;
(Ⅲ)设函数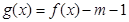 ,试讨论函数
,试讨论函数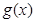 在区间[1,4]上的零点情况.
在区间[1,4]上的零点情况.
已知A(-5,0),B(5,0),动点P满足|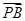 |,
|, |
| |,8成等差数列.
|,8成等差数列.
(1)求P点的轨迹方程;
(2)对于x轴上的点M,若满足| |·|
|·|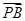 |=
|=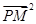 ,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?
,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?
已知函数f(x)=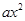 -(a+2)x+lnx.
-(a+2)x+lnx.
(1)当a=1时,求曲线y=f(x)在点(1,f (1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e)上的最小值为-2,求a的取值范围.
在△ABC中,A、B、C为三个内角,a、b、c为相应的三条边,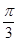 <C<
<C<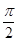 ,且
,且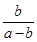 =
=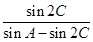 .
.
(1)判断△ABC的形状;
(2)若|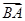 +
+ |=2,求
|=2,求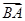 ·
· 的取值范围.
的取值范围.
已知各项均为正数的数列{ }满足
}满足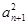 -
- -2
-2 =0,n∈N﹡,且
=0,n∈N﹡,且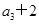 是a2,a4的等差中项.
是a2,a4的等差中项.
(1)求数列{ }的通项公式;
}的通项公式;
(2)若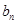 =
=
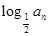 ,
,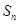 =b1+b2+…+
=b1+b2+…+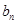 ,求
,求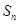 的值.
的值.
已知α,β为锐角,且sinα= ,tan(α-β)=-
,tan(α-β)=- .求cosβ的值.
.求cosβ的值.