如图,已知四棱锥P—ABCD中,底面ABCD为菱形,PA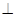 平面ABCD,
平面ABCD,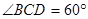 ,BC=1,E为CD的中点,PC与平面ABCD成
,BC=1,E为CD的中点,PC与平面ABCD成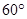 角。
角。
(1)求证:平面EPB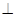 平面PBA;(2)求二面角P-BD-A 的余弦值
平面PBA;(2)求二面角P-BD-A 的余弦值
已知数列 的前
的前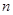 项和
项和 ,正项等比数列
,正项等比数列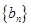 满足:
满足: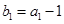 ,且
,且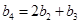 .
.
(Ⅰ)求数列 和
和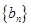 的通项公式;
的通项公式;
(Ⅱ)若数列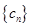 满足:
满足: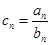 ,求
,求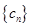 的前
的前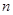 项和
项和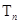 .
.
如图,四棱锥 中,
中, 面
面 ,
, 、
、 分别为
分别为 、
、 的中点,
的中点, ,
, .
.
(1)证明: 面
面 ;
;
(2)求面 与面
与面 所成锐角的余弦值.
所成锐角的余弦值.
甲、乙两名篮球运动员,各自的投篮命中率分别为 与
与 ,如果每人投篮两次.
,如果每人投篮两次.
(Ⅰ)求甲比乙少投进一次的概率;
(Ⅱ)若投进一个球得 分,未投进得
分,未投进得 分,求两人得分之和
分,求两人得分之和 的分布列及数学期望
的分布列及数学期望 .
.
在 中,已知
中,已知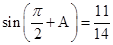 ,
, .
.
(Ⅰ)求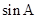 和角
和角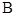 的值;
的值;
(Ⅱ)若角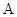 ,
,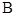 ,
,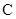 的对边分别为
的对边分别为 ,
, ,
, ,且
,且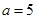 ,求
,求 ,
, 的值.
的值.
已知直线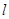 的参数方程为:
的参数方程为: (
( 为参数),曲线
为参数),曲线 的极坐标方程为:
的极坐标方程为: .
.
(1)以极点为原点,极轴为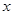 轴正半轴,建立直角坐标系,求曲线
轴正半轴,建立直角坐标系,求曲线 的直角坐标方程;
的直角坐标方程;
(2)若直线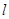 被曲线
被曲线 截得的弦长为
截得的弦长为 ,求
,求 的值.
的值.