定义数列 ,(例如
,(例如 时,
时, )满足
)满足 ,且当
,且当 (
( )时,
)时, .令
.令 .
.
(1)写出数列 的所有可能的情况;
的所有可能的情况;
(2)设 ,求
,求 (用
(用
 的代数式来表示);
的代数式来表示);
(3)求 的最大值.
的最大值.
如图,设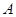 是圆
是圆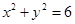 上的动点,点
上的动点,点 是
是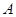 在
在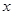 轴上投影,
轴上投影,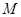 为
为 上一点,且
上一点,且 .当
.当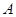 在圆上运动时,点
在圆上运动时,点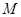 的轨迹为曲线
的轨迹为曲线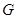 . 过点
. 过点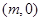
 且倾斜角为
且倾斜角为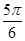 的直线
的直线 交曲线
交曲线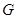 于
于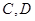 两点.
两点.
(1)求曲线 的方程;
的方程;
(2)若点F是曲线 的右焦点且
的右焦点且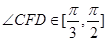 ,求
,求 的取值范围.
的取值范围.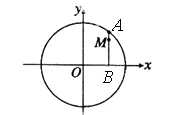
在等差数列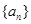 中,
中,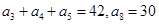 .
.
(1)求数列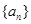 的通项公式;
的通项公式;
(2)若数列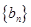 满足
满足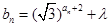 (
( ),则是否存在这样的实数
),则是否存在这样的实数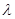 使得
使得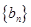 为等比数列;
为等比数列;
(3)数列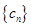 满足
满足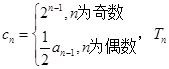 为数列
为数列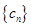 的前n项和,求
的前n项和,求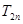 .
.
如图1, 在直角梯形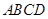 中,
中, 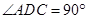 ,
, 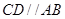 ,
,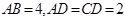 ,
,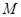 为线段
为线段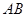 的中点. 将
的中点. 将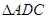 沿
沿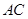 折起,使平面
折起,使平面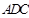
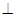 平面
平面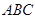 ,得到几何体
,得到几何体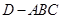 ,如图2所示.
,如图2所示.
(1)求证: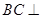 平面
平面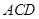 ;
;
(2)求二面角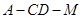 的余弦值.
的余弦值.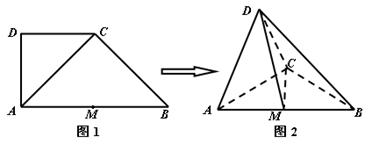
2012年10月莫言获得诺贝尔文学奖后,其家乡山东高密政府准备投资6.7亿元打造旅游带,包括莫言旧居周围的莫言文化体验区,红高粱文化休闲区,爱国主义教育基地等;为此某文化旅游公司向社会公开征集旅游带建设方案,在收到的方案中甲、乙、丙三个方案引起了专家评委的注意,现已知甲、乙、丙三个方案能被选中的概率分别为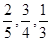 ,且假设各自能否被选中是无关的.
,且假设各自能否被选中是无关的.
(1)求甲、乙、丙三个方案只有两个被选中的概率;
(2)记甲、乙、丙三个方案被选中的个数为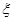 ,试求
,试求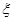 的期望.
的期望.
已知函数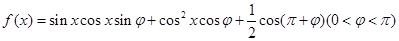 ,其图象过点
,其图象过点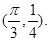
(1)求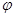 的值;
的值;
(2)将函数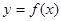 图象上各点向左平移
图象上各点向左平移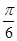 个单位长度,得到函数
个单位长度,得到函数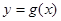 的图象,求函数
的图象,求函数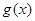 在
在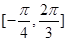 上的单调递增区间.
上的单调递增区间.