下图中,是木杆和旗杆竖在操场上,其中木杆在阳光下的影子已画出.
(1)用线段表示这一时刻旗杆在阳光下的影子.
(2)比较旗杆与木杆影子的长短.
(3)图中是否出现了相似三角形?
(4)为了出现这样的相似三角形,木杆不可以放在图中的哪些位置?
如图,在△ABC中,∠C=90°,D、E、F分别为AB,BC,AC上的中点,求证:CD=EF(8′)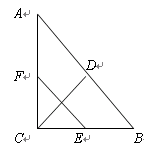
已知三点A、B、C,用直尺和圆规作⊙O,使⊙O过点A、B、C。(不写作法,保留痕迹)(6′)
化简,计算,解方程。
(1) 5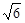 (3
(3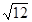 + 4
+ 4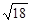 )
)
(2)已知x = + 1,求x² -2x-3的值。
(3)(x+3)2=2x+5
(4)x²-5x+2=0
顾客李某于今年“五·一”期间到电器商场购买空调,与营业员有如下的一段对话:
顾客李某:A品牌的空调去年“国庆”期间价格为3000元,这次便宜多了,一次就降为2430元,是不是质量有问题?
营业员:不是一次降价,这是第二次降价,今年春节期间已经降了一次价,两次降价的幅度相同.我们所销售的空调质量都是很好的,尤其是A品牌系列空调的质量是一流的.
顾客李某:我们单位的同事也想买一台A品牌的空调,有优惠政策吗?
营业员:有,请看《购买A品牌系列空调的优惠办法》.购买A品牌系列空调的优惠办法:
方案一:各种型号的空调每台价格优惠5%,送货上门,负责安装,每台空调另加运输费和安装费共90元.
方案二:各种型号的空调每台价格优惠2%,送货上门,负责安装,免运输费和安装费.根据以上对话和A品牌系列空调销售的优惠办法,请你回答下列问题:
(1)求A品牌系列空调平均每次降价的百分率?
(2)请你为顾客李某决策,选择哪种优惠更合算,并通过计算说明。
已知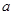 、
、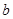 、
、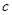 是△ABC的三条边,关于
是△ABC的三条边,关于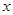 的一元二次方程
的一元二次方程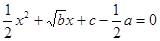 有两个相等的实数根,方程
有两个相等的实数根,方程 的根为x=0。
的根为x=0。
(1)试判断△ABC的形状。
(2)若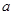 、
、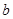 为关于x的一元二次方程x2 +mx-3m=0的两个根,求m的值。
为关于x的一元二次方程x2 +mx-3m=0的两个根,求m的值。