某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为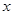 (0<
(0<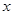 <1
<1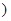 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7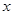 ,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(1)若年销售量增加的比例为0.4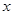 ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例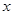 应在什么范围内?
应在什么范围内?
(2)年销售量关于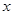 的函数为
的函数为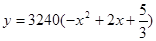 ,则当
,则当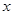 为何值时,本年度的年利润最大?最大利润为多少?
为何值时,本年度的年利润最大?最大利润为多少?
设函数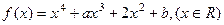 ,其中
,其中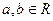
(1)当 时,讨论函数f(x)的单调性;
时,讨论函数f(x)的单调性;
(2)若函数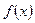 仅在
仅在 处有极值,求
处有极值,求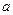 的取值范围;
的取值范围;
(3)若对于任意的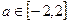 ,不等式
,不等式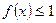 在[-1,1]上恒成立,求b的取值范围.
在[-1,1]上恒成立,求b的取值范围.
已知各项均为正数的数列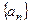 前
前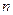 项和为
项和为 ,首项为
,首项为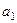 ,且
,且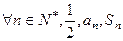 成等差数列.
成等差数列.
(1)求数列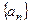 的通项公式;
的通项公式;
(2)若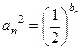 ,设
,设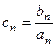 ,求数列
,求数列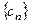 的前
的前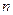 项和
项和 .
.
已知函数
 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(1)求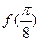 的值;
的值;
(2)将函数y=f(x)的图象向右平移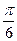 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
已知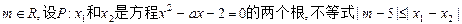 对任意实数
对任意实数 恒成立;Q:函数
恒成立;Q:函数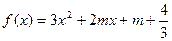 有两个不同的零点. 求使“P∧Q”为真命题的实数m的取值范围.
有两个不同的零点. 求使“P∧Q”为真命题的实数m的取值范围.
在△ABC中,角A,B,C所对的边分别为a,b,c.已知 ,且满足
,且满足 .
.
(1)求角A的大小;
(2)若||+||=||,试判断△ABC的形状.