设函数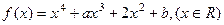 ,其中
,其中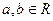
(1)当 时,讨论函数f(x)的单调性;
时,讨论函数f(x)的单调性;
(2)若函数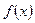 仅在
仅在 处有极值,求
处有极值,求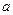 的取值范围;
的取值范围;
(3)若对于任意的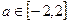 ,不等式
,不等式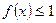 在[-1,1]上恒成立,求b的取值范围.
在[-1,1]上恒成立,求b的取值范围.
设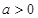 ,集合
,集合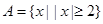 ,
, .
.
(Ⅰ)当a=3时,求集合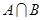 ;
;
(Ⅱ)若 ,求实数
,求实数 的取值范围.
的取值范围.
设函数 ,其中
,其中 。
。
(Ⅰ)若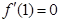 ,求a的值;
,求a的值;
(Ⅱ)当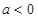 时,讨论函数
时,讨论函数 在其定义域上的单调性;
在其定义域上的单调性;
(Ⅲ)证明:对任意的正整数 ,不等式
,不等式 都成立。
都成立。
请先阅读:
(Ⅰ)利用上述想法(或其他方法),结合等式 (
( ,整数
,整数 ),证明:
),证明: ;
;
(Ⅱ)当整数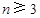 时,求
时,求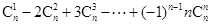 的值;
的值;
(Ⅲ)当整数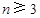 时,证明:
时,证明: .
.
袋中装着标有数字1,2,3,4,5的小球各2个,现从袋中任意取出3个小球,假设每个小球被取出的可能性都相等.
(Ⅰ)求取出的3个小球上的数字分别为1,2,3的概率;
(Ⅱ)求取出的3个小球上的数字恰有2个相同的概率;
(Ⅲ)用X表示取出的3个小球上的最大数字,求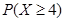 的值.
的值.
设 ,函数
,函数 的导函数为
的导函数为 .
.
(Ⅰ)求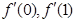 的值,并比较它们的大小;
的值,并比较它们的大小;
(Ⅱ)求函数 的极值.
的极值.