请先阅读:
(Ⅰ)利用上述想法(或其他方法),结合等式 (
( ,整数
,整数 ),证明:
),证明: ;
;
(Ⅱ)当整数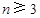 时,求
时,求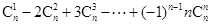 的值;
的值;
(Ⅲ)当整数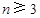 时,证明:
时,证明: .
.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,求
的概率.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,求
的概率.
.(本小题满分12分)在右图所示的多面体中,
下部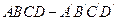 为正方体, 点
为正方体, 点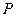 在
在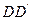 的延长线上,
的延长线上,
且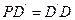 ,
,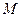 、
、 分别为
分别为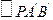 和
和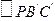 的重心.
的重心.
(1 )已知
)已知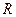 为棱
为棱 上任意一点,求证:
上任意一点,求证: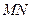 ∥面
∥面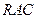 ;
;
(2)求二面角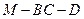 的大
的大 小.
小. 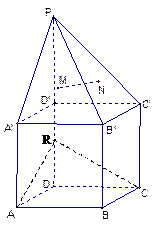
 |
.(本小题满分12分)在△ABC中,内角A、B、C所对边的边长分别为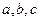 ,
,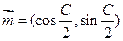 ,
,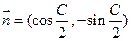 ,且
,且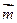 与
与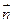 的夹角为
的夹角为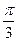 。
。
(1)求内角C;
(2)已知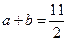 ,且△ABC的面积
,且△ABC的面积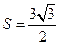 。求
。求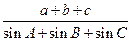 的值。
的值。
.(本小题满分12分)一位客人去北京旅游,他游览长城、故宫、鸟巢这三个景点的概率分别为0.9、0.8、0.8,且他是否游览哪个景点互不影响.设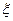 表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.
表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值.
(1)求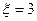 时的概率;
时的概率;
(2)记“函数 在区间
在区间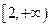 上是增函数”为事件A,求事件A的概率.
上是增函数”为事件A,求事件A的概率.