(1)选修4—4:坐标系与参数方程
已知直线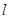 的极坐标方程是
的极坐标方程是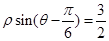 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为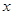 轴的正半轴,建立平面直角坐标系,曲线
轴的正半轴,建立平面直角坐标系,曲线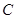 的参数方程是
的参数方程是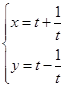 (
(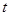 为参数),直线
为参数),直线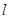 和曲线
和曲线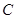 相交于
相交于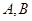 两点,求线段
两点,求线段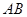 的长.
的长.
(2)选修4—5:不等式选讲
已知正实数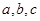 满足
满足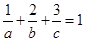 ,求证:
,求证: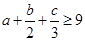 .
.
己知函数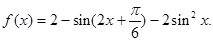
(1)求函数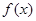 的最小正周期。
的最小正周期。
(2)记△ABC的内角A、B、C的对边长分别为a、b、c,若,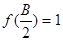 、b=1、c=
、b=1、c=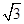 ,求a的值.
,求a的值.
第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
如果存在常数 使得数列
使得数列 满足:若
满足:若 是数列
是数列 中的一项,则
中的一项,则 也是数列
也是数列 中的一项,称数列
中的一项,称数列 为“兑换数列”,常数
为“兑换数列”,常数 是它的“兑换系数”.
是它的“兑换系数”.
(1)若数列: 是“兑换系数”为
是“兑换系数”为 的“兑换数列”,求
的“兑换数列”,求 和
和 的值;
的值;
(2)已知有穷等差数列 的项数是
的项数是 ,所有项之和是
,所有项之和是 ,求证:数列
,求证:数列 是“兑换数列”,并用
是“兑换数列”,并用 和
和 表示它的“兑换系数”;
表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列 ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分6分.
已知点 为双曲线
为双曲线 的左、右焦点,过
的左、右焦点,过 作垂直于
作垂直于 轴的直线,在
轴的直线,在 轴上方交双曲线于点
轴上方交双曲线于点 ,且
,且 ,圆
,圆 的方程为
的方程为 .
.
(1)求双曲线 的方程;
的方程;
(2)过圆 上任意一点
上任意一点 作切线
作切线 交双曲线
交双曲线 于
于 两个不同点,
两个不同点, 中点为
中点为 ,
,
求证: ;
;
(3)过双曲线 上一点
上一点 作两条渐近线的垂线,垂足分别是
作两条渐近线的垂线,垂足分别是 和
和 ,求
,求 的值
的值
第(1)小题满分6分,第(2)小题满分8分.
由于浓酸泄漏对河流形成了污染,现决定向河中投入固体碱。1个单位的固体碱在水中逐步溶化,水中的碱浓度 与时间
与时间 的关系,可近似地表示为
的关系,可近似地表示为 。只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用。
。只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用。
(1)如果只投放1个单位的固体碱,则能够维持有效抑制作用的时间有多长?
(2)当河中的碱浓度开始下降时,即刻第二次投放1个单位的固体碱,此后,每一时刻河中的碱浓度认为是各次投放的碱在该时刻相应的碱浓度的和,求河中碱浓度可能取得的最大值.
第(1)小题满分6分,第(2)小题满分8分.
如图:在正方体 中,
中, 是
是 的中点,
的中点, 是线段
是线段 上一点,且
上一点,且 .
.
(1)求证: ;
;
(2)若平面 平面
平面 ,求
,求 的值.[
的值.[