第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
如果存在常数 使得数列
使得数列 满足:若
满足:若 是数列
是数列 中的一项,则
中的一项,则 也是数列
也是数列 中的一项,称数列
中的一项,称数列 为“兑换数列”,常数
为“兑换数列”,常数 是它的“兑换系数”.
是它的“兑换系数”.
(1)若数列: 是“兑换系数”为
是“兑换系数”为 的“兑换数列”,求
的“兑换数列”,求 和
和 的值;
的值;
(2)已知有穷等差数列 的项数是
的项数是 ,所有项之和是
,所有项之和是 ,求证:数列
,求证:数列 是“兑换数列”,并用
是“兑换数列”,并用 和
和 表示它的“兑换系数”;
表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列 ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
如图,已知正方体 的棱长为2,点
的棱长为2,点 分别为
分别为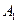
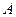 和
和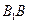 的中点.
的中点.
(Ⅰ)求异面直线CM与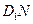 所成角的余弦值;
所成角的余弦值;
(Ⅱ)求点 到平面
到平面 的距离.
的距离.
如图,设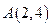 是抛物线
是抛物线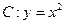 上的一点.
上的一点.
(Ⅰ)求该抛物线 在点A处的切线
在点A处的切线 的方程;
的方程;
(Ⅱ)求曲线C、直线 和
和 轴所围成的图形的面积.
轴所围成的图形的面积.
已知椭圆 的对称轴为坐标轴,焦点是(0,
的对称轴为坐标轴,焦点是(0, ),(0,
),(0,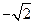 ),又点
),又点
 在椭圆
在椭圆 上.
上.
(1)求椭圆 的方程;
的方程;
(2)已知直线 的斜率为
的斜率为 ,若直线
,若直线 与椭圆
与椭圆 交于
交于 、
、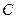 两点,求
两点,求 面积的最大值.
面积的最大值.
图中是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米.
(1)试如图所示建立坐标系,求这条抛物线的方程;
(2)当水下降1米后,水面宽多少?
已知函数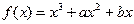 在
在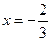 与
与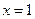 处都取得极值。
处都取得极值。
(1)求函数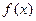
 的解析式;
的解析式;
(2)求函数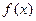 在区间[-2,2]的最大值与最小值。
在区间[-2,2]的最大值与最小值。