( 本小题满分14分)
本小题满分14分)
已知点 ,点
,点 是⊙
是⊙ :
: 上任意两个不同的点,且满足
上任意两个不同的点,且满足 ,设
,设 为弦
为弦 的中点.
的中点.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)试探究在轨迹 上是否存在这样的点:它到直线
上是否存在这样的点:它到直线 的距离恰好等于到点
的距离恰好等于到点 的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
已知函数
(Ⅰ)若 ,求
,求 的极大值;
的极大值;
(Ⅱ)若 在定义域内单调递减,求满足此条件的实数k的取值范围.
在定义域内单调递减,求满足此条件的实数k的取值范围.
已知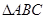 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,
, 是锐角,且
是锐角,且 .
.
(Ⅰ)求 的度数;
的度数;
(Ⅱ)若 ,
,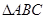 的面积为
的面积为 ,求
,求 的值.
的值.
设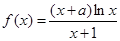 ,曲线
,曲线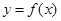 在点
在点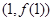 处的切线与直线
处的切线与直线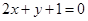 垂直.
垂直.
(1)求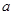 的值;
的值;
(2) 若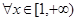 ,
,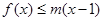 恒成立,求
恒成立,求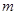 的范围.
的范围.
(3)求证: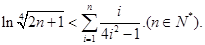
设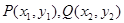 是抛物线
是抛物线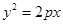
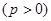 上相异两点,
上相异两点, 到y轴的距离的积为
到y轴的距离的积为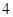 且
且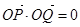 .
.
(1)求该抛物线的标准方程.
(2)过Q的直线与抛物线的另一交点为R,与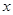 轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为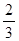 ,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分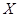 的分布列及数学期望
的分布列及数学期望 ;
;