设 ,函数
,函数 的导函数为
的导函数为 .
.
(Ⅰ)求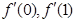 的值,并比较它们的大小;
的值,并比较它们的大小;
(Ⅱ)求函数 的极值.
的极值.
(本小题满分12分)如图,在四棱锥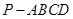 中,底面
中,底面 是菱形,
是菱形,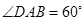 ,
,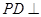 平面
平面 ,
,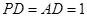 ,点
,点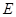 ,
,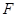 分别为
分别为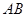 和
和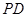 中点.
中点.
(1)求证:直线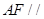 平面
平面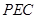 ;
;
(2)求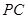 与平面
与平面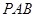 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)已知数列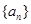 中,
中, ,其前
,其前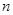 项的和为
项的和为 ,且满足
,且满足
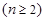 .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)证明:当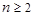 时,
时, .
.
(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=|3x+2|
(Ⅰ)解不等式 ,
,
(Ⅱ)已知m+n=1(m,n>0),若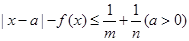 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线M的参数方程为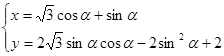 (
( 为参数),若以直角坐标系中的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为
为参数),若以直角坐标系中的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为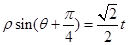 (t为参数).
(t为参数).
(Ⅰ)求曲线M和N的直角坐标方程,
(Ⅱ)若曲线N与曲线M有公共点,求t的取值范围.
(本小题满分10分)选修4--1:几何证明选讲
如图,已知圆O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是圆O的直径.过点C作圆O的切线交BA的延长线于点F.
(Ⅰ)求证:AC·BC="AD·AE;"
(Ⅱ)若AF="2," CF=2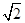 ,求AE的长
,求AE的长