某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次实验,得到数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)作出散点图;
(2)求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)预测加工10个零件需要多少小时?
注:可能用到的公式: ,
, ,
,
如图,四棱锥 ,平面
,平面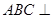 平面
平面 ,
, 边长为
边长为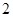 的等边三角形,底面
的等边三角形,底面 是矩形,且
是矩形,且 .
.
(Ⅰ)若点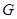 是
是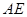 的中点,求证:
的中点,求证: 平面
平面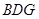 ;
;
(Ⅱ)试问点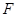 在线段
在线段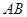 上什么位置时,二面角
上什么位置时,二面角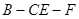 的大小为
的大小为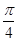 .
.
已知半径为2,圆心在直线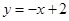 上的圆C.
上的圆C.
(Ⅰ)当圆C经过点A(2,2)且与 轴相切时,求圆C的方程;
轴相切时,求圆C的方程;
(Ⅱ)已知E(1,1),F(1,-3),若圆C上存在点Q,使 ,求圆心的横坐标
,求圆心的横坐标 的取值范围.
的取值范围.
如图,四边形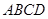 为菱形,
为菱形, 为平行四边形,且面
为平行四边形,且面
 面
面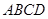 ,
,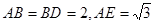 ,设
,设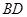 与
与 相交于点
相交于点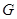 ,
, 为
为 的中点.
的中点.
(Ⅰ)证明: 面
面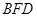 ;
;
(Ⅱ)若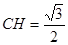 ,求
,求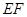 与面
与面 所成角的大小.
所成角的大小.
已知 的顶点
的顶点 ,
,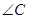 的平分线
的平分线 所在直线方程为
所在直线方程为 ,
, 边上的高
边上的高 所在直线方程为
所在直线方程为 .
.
(Ⅰ)求顶点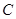 的坐标;
的坐标;
(Ⅱ)求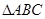 的面积.
的面积.
若某几何体的三视图(单位:cm)如图所示,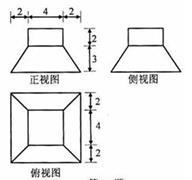
(Ⅰ)求此几何体的表面积;
(Ⅱ)求此几何体的体积.