如图,已知 是长轴为
是长轴为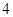 的椭圆上三点,点
的椭圆上三点,点 是长轴的一个顶点,
是长轴的一个顶点, 过椭圆中心
过椭圆中心 ,且
,且 .
.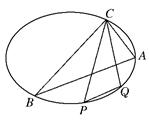
(1)建立适当的坐标系,求椭圆方程;
(2)如果椭圆上两点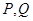 使直线
使直线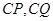 与
与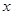 轴围成底边在
轴围成底边在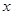 轴上的等腰三角形,是否总存在实数
轴上的等腰三角形,是否总存在实数 使
使 ?请给出证明.
?请给出证明.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,椭圆上的点到焦点的距离的最小值为
轴上,椭圆上的点到焦点的距离的最小值为 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)过点 作直线
作直线 交
交 于
于 、
、 两点,试问:在
两点,试问:在 轴上是否存在一个定点
轴上是否存在一个定点 ,使
,使 为定值?若存在,求出这个定点
为定值?若存在,求出这个定点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知直角梯形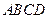 中,
中, ,
,
 过
过 作
作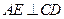 ,垂足为
,垂足为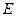 ,
,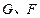 分别为
分别为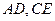 的中点,现将
的中点,现将 沿
沿 折叠使二面角
折叠使二面角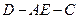 的平面角的正切值为
的平面角的正切值为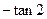 .
.
(1)求证: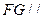 平面
平面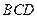 ;
;
(2)求异面直线 与
与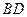 所成的角的余弦值;
所成的角的余弦值;
(3)求二面角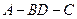 的大小.
的大小.
已知函数 ,数列
,数列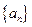 满足
满足 ,
,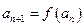 ,
, .
.
(1)求证: ;
;
(2)求证: 是递减数列;
是递减数列;
(3)设 的前
的前 项和为
项和为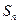 ,
,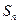 与
与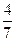 是否有确定的大小关系,如果有给出证明,如果没有给出反例.
是否有确定的大小关系,如果有给出证明,如果没有给出反例.
某校设计了一个实验学科的实验考查方案:考生从 道备选题中一次性随机抽取
道备选题中一次性随机抽取 题,按照题目要求独立完成全部实验操作. 规定:至少正确完成其中
题,按照题目要求独立完成全部实验操作. 规定:至少正确完成其中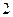 题的便可通过考查.已知
题的便可通过考查.已知 道备选题中考生甲有
道备选题中考生甲有 题能正确完成,
题能正确完成,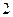 题不能完成;考生乙每题正确完成的概率都是
题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响. 求:
,且每题正确完成与否互不影响. 求:
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
如图所示,某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室,已知已有两面墙的夹角为 (即
(即 ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料 米(两面墙的长均大于
米(两面墙的长均大于 米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记
米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记 ,问当
,问当 为多少时,所建造的三角形露天活动室的面积最大?
为多少时,所建造的三角形露天活动室的面积最大?