对于函数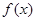
，若存在x0∈R，使方程
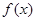成立，则称x0为的不动点，已知函数
（a≠0）．
（1）当
时，求函数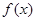的不动点；
（2）若对任意实数b，函数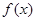恒有两个相异的不动点，求a的取值范围；
试证明：不论正数a、b、c是等差数列还是等比数列，当n＞1,n∈N*且a、b、c互不相等时，均有：an+cn＞2bn.
若n为大于1的自然数，求证：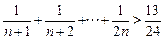
.
已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N,都能使m整除f(n)，求m的最大值。
已知数列{bn}是等差数列，b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+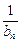
)(其中a＞0且a≠1)记Sn是数列{an}的前n项和，试比较Sn与
logabn+1的大小，并证明你的结论
设实数q满足|q|＜1,数列{an}满足：a1=2,a2≠0,an·an+1=－qn,求an表达式，又如果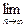
S2n＜3,求q的取值范围