显像管的简要工作原理如图所示：阴极K发出的电子（初速度可忽略不计）经电压为U的高压加速电场加速后，沿直线PQ进入半径为r的圆形匀强磁场区域，磁场方向垂直纸面，圆形磁场区域的圆心O在PQ直线上，荧光屏M与PQ垂直，整个装置处于真空中．若圆形磁场区域内的磁感应强度的大小或方向发生变化，都将使电子束产生不同的偏转，电子束便可打在荧光屏M的不同位置上，使荧光屏发光而形成图象，其中Q点为荧光屏的中心．已知电子的电量为e，质量为m，不计电子重力．
（1）求电子射出加速电场时的速度大小；
（2）若圆形区域的磁场方向垂直纸面向里，磁感应强度大小为B，求电子离开磁场时的偏转（即出射方向与入射方向所夹的锐角）θ的大小．
（3）若阴极在发出电子的同时还发出一定量的SO42－离子，SO42－离子打在荧光屏上，屏上将出现暗斑，称为离子斑．请根据下面所给出的数据，通过计算说明这样的离子斑将主要集中在荧光屏上的哪一部位．（电子的质量m=9.1×10-31kg，SO42－离子的质量m′=1.6×10-25kg，不计SO42－离子所受的重力及与电子之间的相互作用）
用发电机通过如图13所示的输电线路给用户供电，发电机的输出功率为500kW，端电压U1为500V，升压变压器原副线圈的匝数比为1:50，两变压器输电导线的总电阻为1.5Ω，降压变压器的输出电压U4为220V，变压器为理想变压器，求：
①升压变压器副线圈的端电压；
②输电导线上损失的电功率；
③降压变压器原副线圈的匝数比。
如图所示，折射率为
、长为30m的细长透明体放在空气中，光从A端射入沿透明体传播到B端面。求光在透明体中从A端传播到B端所需时间的最小值和最大值。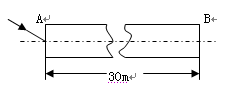
用波长为660nm的红光做双缝干涉实验，相邻两亮条纹间距为4.8nm，
①如果实验装置不变，改用波长为440nm的紫光，相邻两亮条纹间距为多少？
②如果相邻两亮条纹间距是4nm，则实验所用单色光波长为多少？
如图所示，让摆球从图中的A位置开始下摆，正好摆到最低点B位置时线被拉断.设摆线长l,悬点到地面的竖直高度为3l，绳子能承受的最大拉力为5mg，不计空气阻力，求：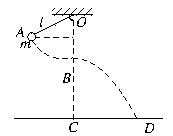
（1）摆球落地时的速度.
（2）落地点D到C点的距离（g＝10 m／s2）.
如图所示，一光滑的半径为R的竖直半圆形轨道固定在水平面上，一个质量为m的小球以某一速度冲上轨道，当小球将要从轨道口飞出时，轨道的压力恰好为零，则小球落地点C距A处多远？