(本小题满分10分)
如图所示是一个半圆柱 与三棱柱
与三棱柱 的组合体,其中,圆柱
的组合体,其中,圆柱 的轴截面
的轴截面 是边长为4的正方形,
是边长为4的正方形,
 为等腰直角三角形,
为等腰直角三角形, .
.
试在给出的坐标纸上画出此组合体的三视图.
已知函数f(x)=ln x-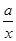 .
.
(1)当a>0时,判断f(x)在定义域上的单调性;
(2)f(x)在[1,e]上的最小值为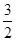 ,求实数a的值;
,求实数a的值;
(3)试求实数a的取值范围,使得在区间(1,+∞)上函数y=x2的图象恒在函数y=f(x)图象的上方.
已知函数f(x)=-2x+4,令Sn=f( )+f(
)+f( )+f(
)+f(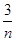 )+…+f(
)+…+f( )+f(1).
)+f(1).
(1)求Sn;
(2)设bn= (a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.
(a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.
为保增长、促发展,某地计划投资甲、乙两项目,市场调研得知,甲项目每投资百万元需要配套电能2万千瓦,可提供就业岗位24个,增加GDP260万元;乙项目每项投资百万元需要配套电能4万千瓦,可提供就业岗位32个,增加GDP200万元,已知该地为甲、乙两项目最多可投资3 000万元,配套电能100万千瓦,并要求它们提供的就业岗位不少于800个,如何安排甲、乙两项目的投资额,增加的GDP最大?
已知向量m=( sin
sin 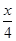 ,1),n=(cos
,1),n=(cos 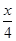 ,cos2
,cos2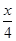 ).记f(x)=m·n.
).记f(x)=m·n.
(1)若f(α)=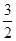 ,求cos(
,求cos( -α)的值;
-α)的值;
(2)在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cos B=bcos C,若f(A)=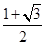 ,试判断△ABC的形状.
,试判断△ABC的形状.
已知函数f(x)= ,数列{an}满足:2an+1-2an+an+1an=0且an≠0.数列{bn}中,b1=f(0)且bn=f(an-1).
,数列{an}满足:2an+1-2an+an+1an=0且an≠0.数列{bn}中,b1=f(0)且bn=f(an-1).
(1)求证:数列 是等差数列;
是等差数列;
(2)求数列{|bn|}的前n项和Tn.