为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有1000名学生参加了这次竞赛．为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请你根据尚未完成的频率分布表和频数分布条形图，解答下列问题：
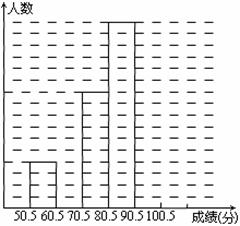
（1）求频率分布表中的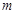
，
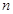值，并补全频数条形图；
（2）根据频数条形图估计该样本的中位数是多少？
（3）若成绩在65.5~85.5分的学生为三等奖，问该校获得三等奖的学生约为多少人？
已知不等式ax2＋bx＋c>0的解集为(1，t)，记函数f(x)＝ax2＋(a－b)x－c.
(1)求证：函数y＝f(x)必有两个不同的零点；
(2)若函数y＝f(x)的两个零点分别为m，n，求|m－n|的取值范围；
(3)是否存在这样的实数a，b，c及t使得函数y＝f(x)在[－2,1]上的值域为[－6,12]？若存在，求出t的值及函数y＝f(x)的解析式；若不存在，请说明理由．
设二次函数f(x)＝ax2＋bx＋c，函数F(x)＝f(x)－x的两个零点为m，n(m<n)．
(1)若m＝－1，n＝2，求不等式F(x)>0的解集；
(2)若a>0，且0<x<m<n<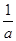
，比较f(x)与m的大小．
设a≠0，对于函数f(x)＝log3(ax2－x＋a)，
(1)若函数f(x)的定义域为R，求实数a的取值范围；
(2)若函数f(x)的值域为R，求实数a的取值范围．
已知关于x的不等式kx2－2x＋6k<0(k≠0)．
(1)若不等式的解集为{x|x<－3或x>－2}，求k的值；
(2)若不等式的解集为{x|x∈R，x≠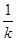
}，求k的值；
(3)若不等式的解集为R，求k的取值范围；
(4)若不等式的解集为∅，求k的取值范围．
已知a，b，c∈{正实数}，且a2＋b2＝c2，当n∈N，n>2时比较cn与an＋bn的大小．