(原创)已知焦点在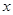 轴上,中心在坐标原点的椭圆C经过点
轴上,中心在坐标原点的椭圆C经过点
(Ⅰ)求椭圆C的短轴长的取值范围;
(Ⅱ)若椭圆C的离心率为 ,且直线
,且直线 分别切椭圆C与圆
分别切椭圆C与圆 (其中
(其中 )于A、B两点,求|AB|的最大值.
)于A、B两点,求|AB|的最大值.
(本小题满分13分)
设命题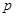 :关于x的函数
:关于x的函数 为增函数;命题
为增函数;命题 :不等式
:不等式 对一切正实数均成立.
对一切正实数均成立.
(1)若命题 为真命题,求实数
为真命题,求实数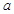 的取值范围;
的取值范围;
(2)命题“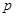 或
或 ”为真命题,且“
”为真命题,且“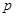 且
且 ”为假命题,求实数
”为假命题,求实数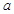 的取值范围.
的取值范围.
(本小题满分13分)
已知集合 ,
, 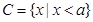 .
.
(1)求 和
和 ;(2)若
;(2)若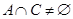 ,求
,求 的取值范围.
的取值范围.
已知函数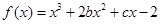 的图象在与
的图象在与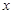 轴交点处的切线方程是
轴交点处的切线方程是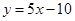 .
.
(I)求函数 的解析式;
的解析式;
(II)设函数 ,若
,若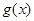 的极值存在,求实数
的极值存在,求实数 的取值范围以及函数
的取值范围以及函数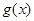 取得极值时对应的自变量
取得极值时对应的自变量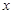 的值.
的值.
已知二次函数 函数
函数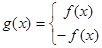

(1)若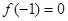 且函数
且函数 恒成立,求
恒成立,求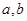 的值;
的值;
(2)在(1)的条件下,当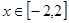 时,
时, 是单调函数,求
是单调函数,求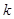 的取值范围.
的取值范围.
(3)若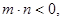
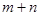 >0,
>0,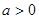 且
且 为偶函数,判断
为偶函数,判断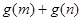 的符号(正或负)
的符号(正或负)
并说明理由.
已知函数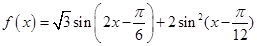 +2m-1
+2m-1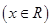 .
.
(1)求函数 的单调递增区间.
的单调递增区间.
(2)若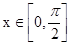 函数
函数 取得最小值为5,求m的值.
取得最小值为5,求m的值.