已知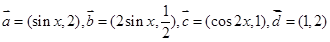 ,又二次函数
,又二次函数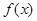 的图象是开口向上,其对称轴为
的图象是开口向上,其对称轴为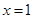 的抛物线,当
的抛物线,当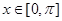 时,求使不等式
时,求使不等式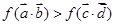 成立的x的取值范围
成立的x的取值范围
如图,椭圆C0: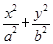 =1(a>b>0,a、b为常数),动圆C1:x2+y2=
=1(a>b>0,a、b为常数),动圆C1:x2+y2=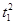 ,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
(1)求直线AA1与直线A2B交点M的轨迹方程;
(2)设动圆C2:x2+y2= 与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: 为定值.
为定值.
如图,在平面直角坐标系xOy中,椭圆的中心在原点O,右焦点F在x轴上,椭圆与y轴交于A、B两点,其右准线l与x轴交于T点,直线BF交椭圆于C点,P为椭圆上弧AC上的一点.
(1)求证:A、C、T三点共线;
(2)如果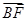 =3
=3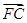 ,四边形APCB的面积最大值为
,四边形APCB的面积最大值为 ,求此时椭圆的方程和P点坐标.
,求此时椭圆的方程和P点坐标.
如图,椭圆C: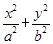 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 .不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
.不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.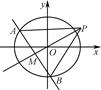
(1)求椭圆C的方程;
(2)求△ABP面积取最大值时直线l的方程.
已知椭圆 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且过点P
,且过点P ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
过Q作平行于x轴的直线交直线AP于点M,以QM为直径的圆的圆心为N.
(1)求椭圆方程;
(2)若圆N与x轴相切,求圆N的方程;
(3)设点R为圆N上的动点,点R到直线PF的最大距离为d,求d的取值范围.
已知椭圆 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴的一个端点为M(0,1),直线l:y=kx-
,短轴的一个端点为M(0,1),直线l:y=kx-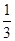 与椭圆相交于不同的两点A、B.
与椭圆相交于不同的两点A、B.
(1)若AB= ,求k的值;
,求k的值;
(2)求证:不论k取何值,以AB为直径的圆恒过点M.