已知函数f (x)=-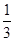 ax3+
ax3+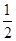 x2+(a-1)x-
x2+(a-1)x-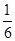 (x>0),(aÎR).
(x>0),(aÎR).
(Ⅰ)当0<a<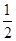 时,讨论f (x)的单调性;
时,讨论f (x)的单调性;
(Ⅱ)若f (x)在区间(a, a+1)上不具有单调性,求正实数a的取值范围.
已知向量a=(cosθ,sinθ),θ∈[0,π],向量b=( ,-1).
,-1).
(1)若a⊥b,求θ的值;
(2)若|2a-b|<m恒成立,求实数m的取值范围.
已知点O(0,0)、A(1,2)、B(4,5)及 =
= +t
+t ,试问:
,试问:
(1)t为何值时,P在x轴上?在y轴上?P在第三象限?
(2)四边形OABP能否成为平行四边形?若能,求出相应的t值;若不能,请说明理由.
已知向量a=(1,2),b=(2,-2).
(1)设c=4a+b,求(b·c)a;
(2)若a+λb与a垂直,求λ的值;
(3)求向量a在b方向上的投影.
已知点G是△ABO的重心,M是AB边的中点.
(1)求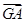 +
+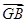 +
+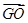 ;
;
(2)若PQ过△ABO的重心G,且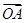 =a,
=a, =b,
=b,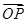 =ma,
=ma,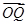 =nb,求证:
=nb,求证: +
+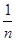 =3.
=3.
设i、j分别是平面直角坐标系Ox,Oy正方向上的单位向量,且 =-2i+mj,
=-2i+mj, =ni+j,
=ni+j,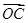 =5i-j,若点A、B、C在同一条直线上,且m=2n,求实数m、n的值.
=5i-j,若点A、B、C在同一条直线上,且m=2n,求实数m、n的值.