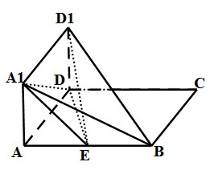
已知点G是△ABO的重心,M是AB边的中点.
(1)求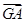 +
+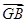 +
+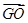 ;
;
(2)若PQ过△ABO的重心G,且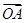 =a,
=a, =b,
=b,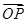 =ma,
=ma,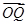 =nb,求证:
=nb,求证: +
+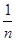 =3.
=3.
(1)已知a>b>c,且a+b+c=0,用分析法求证:<a.
(2)f(x)=,先分别求f(0)+f(1),f(-1)+f(2),f(-2)+f(3),然后归纳猜想一般性结论,并给出证明.
已知函数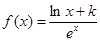 (k为常数,e=2.71828…是自然对数的底数),曲线
(k为常数,e=2.71828…是自然对数的底数),曲线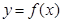 在点
在点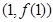 处的切线与x轴平行.
处的切线与x轴平行.
(1)求k的值及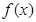 的单调区间;
的单调区间;
(2)设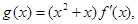 其中
其中 为
为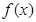 的导函数,证明:对任意
的导函数,证明:对任意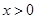 ,
, .
.
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,
以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求:
(1)打满3局比赛还未停止的概率;
(2)比赛停止时已打局数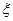 的分别列与期望E
的分别列与期望E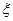 .
.
已知函数 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.
(1)求函数f(x)的解析式;
(2)求函数 的值域.
的值域.
如图所示,正方形 与矩形
与矩形 所在平面互相垂直,
所在平面互相垂直,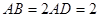 ,点
,点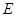 为
为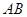 的中点.
的中点.
(1)求证: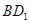 ∥平面
∥平面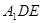 ;(2)求证:
;(2)求证: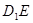
 ;
;
(3)在线段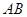 上是否存在点
上是否存在点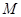 ,使二面角
,使二面角 的大小为
的大小为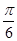 ?若存在,求出
?若存在,求出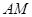 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.