在正三棱锥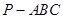 中,
中,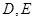 分别是
分别是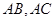 的中点,有下列三个论断:
的中点,有下列三个论断:
①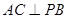 ;②
;②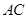 //平面
//平面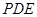 ;③
;③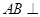 平面
平面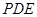 ,
,
其中正确论断的个数为 ( )
| A.3个 | B.2个 | C.1个 | D.0个 |
长方形桌球台的长和宽之比为7:5,某人从一个桌角处沿45o角将球打到对边,然后经过n次碰撞,最后落到对角,则n=()
| A.8 | B.9 | C.10 | D.12 |
如果命题P: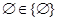 ,命题Q:
,命题Q: ,那么下列结论不正确的是
,那么下列结论不正确的是
| A.“P或Q”为真 | B.“P且Q”为假 |
| C.“非P”为假 | D.“非Q”为假 |
设
| A.a<b<c | B.a<c<b | C.c<b<a | D.b<a<c |
在等差数列{an}中,a1=1,a7=4,数列{bn}是等比数列,且b1=6,b2=a3,则满足bna26<1的最小整数n是()
| A.4 | B.5 | C.6 | D.7 |
已知映射 ,其中A=B=R,对应法则
,其中A=B=R,对应法则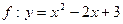 ,
, ,对于集合B中的元素1,下列说法正确的是:()
,对于集合B中的元素1,下列说法正确的是:()
| A.在A中有1个原象 | B.在A中有2个原象 |
| C.在A中有3个原象 | D.在A中没有原象 |