(本小题满分12分)
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形,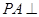 平面
平面 ,
, ,
,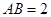 .
.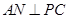 于点
于点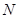 ,
,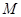 是
是 中点.
中点.
(1)用空间向量证明:AM⊥MC,平面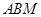 ⊥平面
⊥平面 ;
;
(2)求直线 与平面
与平面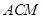 所成的角的正弦值;
所成的角的正弦值;
(3)求点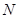 到平面
到平面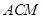 的距离.
的距离.
(本小题满分14分)
已知点C(1,0),点A、B是⊙O: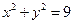 上任意两个不同的点,且满足
上任意两个不同的点,且满足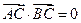 ,设P为弦AB的中点.
,设P为弦AB的中点.
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线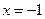 的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.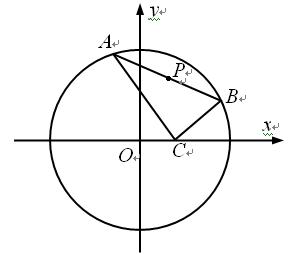
(本小题满分14分)
如图,四边形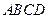 为矩形,且
为矩形,且 ,
,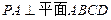 ,
, 为
为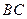 上的动点.
上的动点.
(1) 当 为
为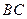 的中点时,求证:
的中点时,求证: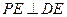 ;
;
(2) 设 ,在线段
,在线段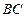 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角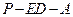 的平面角大小为
的平面角大小为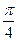 . 试确定点E的位置.
. 试确定点E的位置.
(本小题满分12分)
一个口袋中装有大小相同的2个白球和3个黑球.
(1)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(2)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的分布列与期望。
(本小题满分 分)
分)
设三角形 的内角
的内角 的对边分别为
的对边分别为
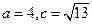 ,
,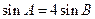 .
.
(1)求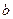 边的长;
边的长;
(2)求角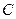 的大小;
的大小;
(3)求三角形 的面积
的面积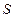 。
。
(本小题满分12分)已知二次函数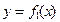 的
的 图象以原点为顶点且过点(1,1),反比例函数
图象以原点为顶点且过点(1,1),反比例函数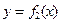 的图象与直线
的图象与直线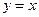 的两个交点间的距离为8,
的两个交点间的距离为8,
(1)求函数 的表达式;
的表达式;
(2)证明:当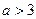 时,关于
时,关于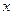 的方程
的方程 有三个实数解.
有三个实数解.