在双曲线 中,F1、F2分别为其左右焦点,点P在双曲线上运动,求△PF1F2的重心G的轨迹方程.
中,F1、F2分别为其左右焦点,点P在双曲线上运动,求△PF1F2的重心G的轨迹方程.
某人抛掷一枚质量分布均匀的骰子,出现各数的概率都是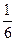 ,构造数列
,构造数列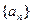 ,使
,使
 ,记
,记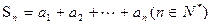 .
.
(Ⅰ)求 时的概率;
时的概率;
(Ⅱ)求前两次均为奇数且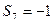 的概率.
的概率.
已知数列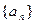 的首项
的首项 ,前
,前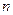 项和
项和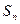 恒为正数,且当
恒为正数,且当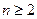 时,
时,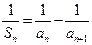 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求证: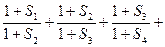
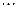
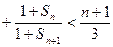 .
.
已知点 满足:
满足: (其中
(其中 ,又知
,又知 .
.
(Ⅰ)若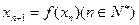 ,求
,求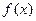 的表达式;
的表达式;
(Ⅱ)已知点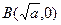 记
记 ,且
,且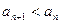 对一切
对一切 恒成立,试求
恒成立,试求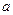 的取值范围;
的取值范围;
(Ⅲ)设(2)中的数列 的前
的前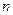 项和为
项和为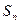 ,试证:
,试证: .
.
如图, 是抛物线
是抛物线 的焦点,
的焦点, 为准线与
为准线与 轴的交点,直线
轴的交点,直线 经过点
经过点 .
.
(Ⅰ)直线 与抛物线有唯一公共点,求
与抛物线有唯一公共点,求 的方程;
的方程;
|
(Ⅱ)直线 与抛物线交于
与抛物线交于 、
、 两点记
两点记 、
、 的斜率分别为
的斜率分别为 ,
, .
.
 为定值;
为定值;
 在线段
在线段 上,且满足
上,且满足
 ,求点
,求点 的轨迹方程.
的轨迹方程.
函数 .
.
(Ⅰ)当 时,求
时,求 的最小值;
的最小值;
(Ⅱ)当 时,求
时,求 的单调区间.
的单调区间.