某中学库存960套旧课桌椅准备修理。现有甲、乙两个木工小组都想承接这项业务。经协商后得知:甲小组单独修理这批桌椅比乙小组多用20天;乙小组每天比甲小组多修8套;学校每天需付甲小组修理费80元,付乙小组120元。
(1)求甲、乙两个小组每天各修理桌櫈多少套?
(2)在修理过程中,学校要委派一名修理工进行质量监督,并由学校负担他每天的生活补助10元,现有以下三种修理方案供选择:①由甲单独修理;②由乙单独修理;③由甲、乙共同合作修理。你认为哪种方案既省时又省钱?试比较说明。
某运输公司有 、 两种货车,3辆 货车与2辆 货车一次可以运货90吨,5辆 货车与4辆 货车一次可以运货160吨.
(1)请问1辆 货车和1辆 货车一次可以分别运货多少吨?
(2)目前有190吨货物需要运输,该运输公司计划安排 、 两种货车将全部货物一次运完 、 两种货车均满载),其中每辆 货车一次运货花费500元,每辆 货车一次运货花费400元.请你列出所有的运输方案,并指出哪种运输方案费用最少.
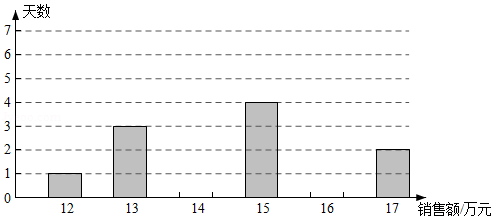
某合作社为帮助农民增收致富,根据网络平台销售当地的一种农副产品.为了解该农副产品在一个季度内每天的销售额,从中随机抽取了20天的销售额(单位:万元)作为样本,数据如下:
16 14 13 17 15 14 16 17 14 14
15 14 15 15 14 16 12 13 13 16
(1)根据上述样本数据,补全条形统计图;
(2)上述样本数据的众数是 ,中位数是 ;
(3)根据样本数据,估计这种农副产品在该季度内平均每天的销售额.
化简: .
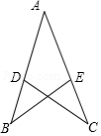
如图,点 在 上,点 在 上, , ,求证: .
计算: .