小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径OB=3cm,高OC=4cm,求这个圆锥形漏斗的侧面积.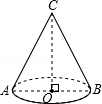
已知圆锥的底面直径是8,母线长是16,求它的侧面展开图的圆心角与圆锥的全面积.
如图,已知每个小正方形的边长为1cm,O、A、B都在小正方形顶点上,扇形OAB是某个圆锥的侧面展开图.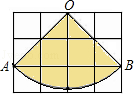
(1)计算这个圆锥侧面展开图的面积;
(2)求这个圆锥的底面半径.
如图,已知在⊙O中,AB=4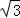 ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
,AC是⊙O的直径,AC⊥BD于F,∠A=30°.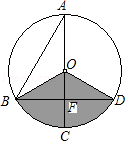
(1)求图中阴影部分的面积;
(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.
(3)试判断⊙O中其余部分能否给(2)中的圆锥做两个底面.
如图,一只纺锤可近似看作由两个圆锥拼合而成,AB=18,AD=9,r=3.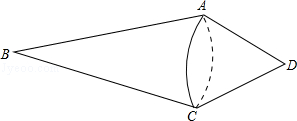
(1)求纺锤的表面积;
(2)一只蚂蚁要从C点出发绕这只纺锤爬一圈回到原地,求蚂蚁爬过的最短路线长.