已知椭圆 的方程为
的方程为 ,双曲线
,双曲线 的两条渐近线为
的两条渐近线为 ,
, ,过椭圆
,过椭圆 的右焦点
的右焦点 作直线
作直线 ,使
,使 ⊥
⊥ ,又l与
,又l与 交于
交于 点,设
点,设 与椭圆
与椭圆 的两个交点由上至下依次为
的两个交点由上至下依次为 .
.
(1)当 与
与 夹角为60°,双曲线的焦距为4时,求椭圆
夹角为60°,双曲线的焦距为4时,求椭圆 的方程及离心率;
的方程及离心率;
(2)求 的最大值.
的最大值.
已知抛物线的顶点在原点,焦点在 轴正半轴上,抛物线上一点的横坐标为2,且该点到焦点的距离为2.
轴正半轴上,抛物线上一点的横坐标为2,且该点到焦点的距离为2.
(1)求抛物线的标准方程;
(2)与圆 相切的直线
相切的直线 交抛物线于不同的两点
交抛物线于不同的两点 ,若抛物线上一点
,若抛物线上一点 满足
满足 ,求
,求 的取值范围。
的取值范围。
已知“ ,使等式
,使等式 成立”是真命题.
成立”是真命题.
(1)求实数 的取值集合
的取值集合 ;
;
(2)设不等式 解集为
解集为 ,若
,若 是
是 的必要条件,求实数
的必要条件,求实数 的取值范围.
的取值范围.
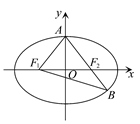
如图,已知椭圆 ,
,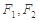 分别为椭圆的左、右焦点,
分别为椭圆的左、右焦点,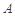 为椭圆的上顶点,直线
为椭圆的上顶点,直线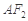 交椭圆于另一点
交椭圆于另一点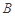 .
.
(1)若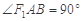 ,求椭圆的离心率;
,求椭圆的离心率;
(2)若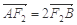 ,
, ,求椭圆的方程.
,求椭圆的方程.
设命题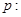
 和
和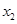 是方程
是方程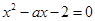 的两个根,不等式
的两个根,不等式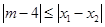 对任意实数
对任意实数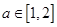 恒成立;命题Q:函数
恒成立;命题Q:函数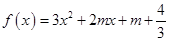 有两个不同的零点.求使“P且Q”为真命题的实数
有两个不同的零点.求使“P且Q”为真命题的实数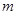 的取值范围.
的取值范围.