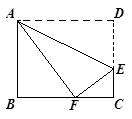甲乙二人同时从张庄出发,步行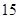 千米到李庄,甲比乙每小时多走
千米到李庄,甲比乙每小时多走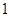 千米,结果比乙早到半小时.问二人每小时各走几千米?
千米,结果比乙早到半小时.问二人每小时各走几千米?
如图13,□ABCD中,BD⊥AB,AB=12cm,AC=26cm,求AD、BD长.
如图,四边形ABCD为菱形,A(0,4),B(﹣3,0).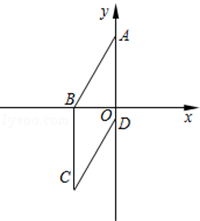
(1)求点D的坐标
(2)求经过C点的反比例函数解析式.
(本小题7分)如图1,已知 是等腰直角三角形,
是等腰直角三角形,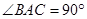 ,点
,点 是
是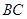 的中点.作
的中点.作
正方形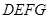 ,使点
,使点 、
、 分别在
分别在 和
和 上,连接
上,连接 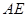 ,
, .
.
(1)试猜想线段 和
和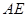 的数量关系是 并证明.
的数量关系是 并证明.
(2)将正方形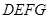 绕点
绕点 逆时针方向旋转
逆时针方向旋转 ,判断(1)中的结论是否仍然成立?请利用图2证明你的结论;
,判断(1)中的结论是否仍然成立?请利用图2证明你的结论;
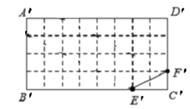
(本小题5分)我们定义:如图1,矩形MNPQ中,点K、O、G、H分别在NP、PQ、QM、MN上,若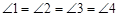 ,则称四边形KOGH为矩形MNPQ的反射四边形.如图2、图3四边形ABCD、A’B’C’D’均为矩形,它们都是由32个边长为1的正方形组成的图形,点E、F、E’、F’分别在BC、CD、B’C’、C’D’边上,试利用正方形网格在图2、图3中分别画出矩形ABCD和矩形A’B’C’D’的反射四边形EFGH和E’F’G’H’.
,则称四边形KOGH为矩形MNPQ的反射四边形.如图2、图3四边形ABCD、A’B’C’D’均为矩形,它们都是由32个边长为1的正方形组成的图形,点E、F、E’、F’分别在BC、CD、B’C’、C’D’边上,试利用正方形网格在图2、图3中分别画出矩形ABCD和矩形A’B’C’D’的反射四边形EFGH和E’F’G’H’.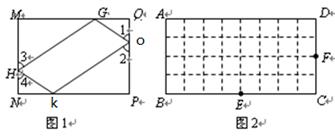
(本小题5分)如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6cm,AB=16,求BF的长.