如图所示,正方形线框abcd放在光滑绝缘的水平面上,其边长L=0.5m、质量m=0.5kg、电阻R=0.5Ω,M、N分别为线框ad、bc边的中点.图示两个虚线区域内分别有竖直向下和向上的匀强磁场,磁感应强度均为B=1T,PQ为其分界线.线框从图示位置以速度v0=2m/s匀速向右滑动,当MN与PQ重合时,线框的速度v1=1m/s,此时立刻对线框施加一沿运动方向的水平拉力,使线框匀速运动直至完全进入右侧匀强磁场区域.求:

(1)线框由图示位置运动到MN与PQ重合的过程中磁通量的变化量;
(2)线框运动过程中最大加速度的大小;
(3)线框在图示位置起直至完全进入右侧匀强磁场区域运动过程中,线框中产生的焦耳热.
如图所示,真空中有一半径r=0.5 m的圆形磁场区域,圆与x轴相切于坐标原点O,磁场的磁感应强度大小B=2×10-3 T,方向水平向里,在x1=0.5 m到x2=1.0 m区域内有一个方向竖直向下的匀强电场,电场强度E=2.0×103 N/C.在x=2.0 m处有竖直放置的一足够大的荧光屏.现将比荷为=1×109 C/kg的带负电粒子从O点处射入磁场,不计粒子所受重力.(sin37°=0.6,cos37°=0.8)
(1)若粒子沿y轴正方向射入,恰能从磁场与电场的相切处进入电场,求粒子最后到达荧光屏上位置的y的坐标.
(2)若粒子以(1)问中相同速率从O点与y轴成37°角射入第二象限,求粒子到达荧光屏上位置的y坐标.
福建省“十二五”水利发展规划指出,若按现有供水能力测算,我省供水缺口极大,蓄引提水是目前解决供水问题的重要手段之一.某地要把河水抽高20m,进入蓄水池,用一台电动机通过传动效率为80%的皮带,带动效率为60%的离心水泵工作.工作电压为380V,此时输入电动机的电功率为19kW,电动机的内阻为0.4Ω.已知水的密度为1×103kg/m3,重力加速度取10m/s2.求:
(1)电动机内阻消耗的热功率;
(2)将蓄水池蓄入864m3的水需要的时间(不计进、出水口的水流速度).
如图所示的装置,左半部为速度选择器,右半部为匀强的偏转电场。一束同位素离子流从狭缝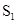 射入速度选择器,能够沿直线通过速度选择器并从狭缝
射入速度选择器,能够沿直线通过速度选择器并从狭缝 射出的离子,又沿着与电场垂直的方向,立即进入场强大小为
射出的离子,又沿着与电场垂直的方向,立即进入场强大小为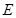 的偏转电场,最后打在照相底片
的偏转电场,最后打在照相底片 上。已知同位素离子的电荷量为
上。已知同位素离子的电荷量为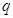 (
(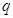 >0),速度选择器内部存在着相互垂直的场强大小为
>0),速度选择器内部存在着相互垂直的场强大小为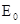 的匀强电场和磁感应强度大小为
的匀强电场和磁感应强度大小为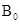 的匀强磁场,照相底片D与狭缝
的匀强磁场,照相底片D与狭缝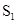 、
、 连线平行且距离为L,忽略重力的影响。
连线平行且距离为L,忽略重力的影响。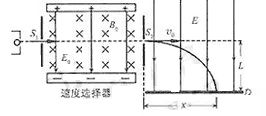
(1)求从狭缝 射出的离子速度
射出的离子速度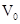 的大小;
的大小;
(2)若打在照相底片上的离子在偏转电场中沿速度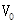 方向飞行的距离为
方向飞行的距离为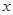 ,求出
,求出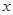 与离子质量
与离子质量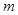 之间的关系式(用
之间的关系式(用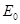 、
、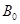 、
、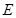 、
、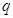 、
、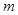 、L表示)。
、L表示)。
质量为 、长为
、长为 的长木板静止在光滑水平面上;质量也为
的长木板静止在光滑水平面上;质量也为 的小滑块(可看做质点),放在长木板的左端,如图所示;给小滑块一水平向右的拉力
的小滑块(可看做质点),放在长木板的左端,如图所示;给小滑块一水平向右的拉力 ;当
;当 取不同值时求解下列问题。(重力加速度为
取不同值时求解下列问题。(重力加速度为 )
)
(1)使滑块在木板上发生相对滑动, 至少为多大;
至少为多大;
(2)当 时,经多长时间,力
时,经多长时间,力 可使滑块滑至木板的最右端;
可使滑块滑至木板的最右端;
(3)当 时,
时, 至少作用多长时间后再撤去,最终滑块可以滑到木板的最右端。
至少作用多长时间后再撤去,最终滑块可以滑到木板的最右端。
如图所示,匀速转动的水平转台上,沿半径方向放置两个用细线相连的小物块A、B(可视为质点),质量分别为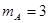 kg、
kg、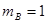 kg;细线长
kg;细线长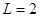 m,A、B与转台间的动摩擦因数
m,A、B与转台间的动摩擦因数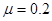 。开始转动时A放在转轴处,细线刚好拉直但无张力, 重力加速度
。开始转动时A放在转轴处,细线刚好拉直但无张力, 重力加速度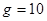 m/s2。最大静摩擦力等于滑动摩擦力,求:
m/s2。最大静摩擦力等于滑动摩擦力,求: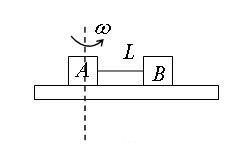
(1)使细线刚好拉直但无张力,转台转动的最大角速度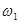 为多少;
为多少;
(2)使A、B能随转台一起匀速圆周运动,转台转动的最大角速度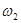 为多少
为多少