数列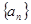 的各项均为正数,
的各项均为正数,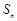 为其前
为其前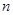 项和,对于任意
项和,对于任意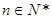 ,总有
,总有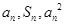 成等差数列.
成等差数列.
(Ⅰ)求数列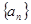 的通项公式;
的通项公式;
(Ⅱ)设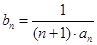 ,求数列
,求数列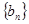 的前
的前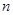 项和
项和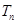 .
.
(本小题满分12分)某射击运动员在一次射击中,命中10环、9环、8环、7环的概率分别为0.2、0.35、0.2、0.15。求此运动员
(1)在一次射击中,命中10环或9环的概率。
(2)在一次射击中,命中环数小于8环的概率。
(3)在两次射击中,至少有一次击中10环的概率。
(本小题满分12分)已知函数 ,输入自变量
,输入自变量 的值,输出对应的函数值
的值,输出对应的函数值 。(1)画出算法框图。(2)写出程序语句。
。(1)画出算法框图。(2)写出程序语句。
(12分)已知函数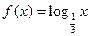 ,
,
(1)当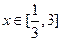 时,求
时,求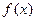 的反函数
的反函数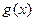 ;
;
(2)求关于 的函数
的函数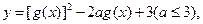 当
当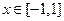 时的最小值
时的最小值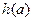 ;
;
(3)我们把同时满足下列两个性质的函数称为“和谐函数”: ①函数在整个定义域上是单调增函数或单调减函数;②在函数的定义域内存在区间
①函数在整个定义域上是单调增函数或单调减函数;②在函数的定义域内存在区间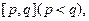 使得函数在区间
使得函数在区间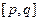 上的值域为
上的值域为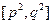 .
. (Ⅰ)判断(2)中
(Ⅰ)判断(2)中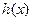 是否为“和谐函数”?若是,求出
是否为“和谐函数”?若是,求出 的值或关系式;若不是,请说明理由;
的值或关系式;若不是,请说明理由;
(Ⅱ)若关于 的函数
的函数 是“和谐函数”,求实数
是“和谐函数”,求实数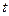 的取值范围.
的取值范围.
(12分)已知函数 ,
,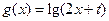 (
(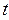 为参数)
为参数)
(1)当函数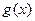 在
在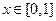 上恒有意义时,求实数
上恒有意义时,求实数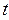 的取值范围;
的取值范围;
(2)如果当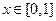 时,
时,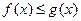 恒成立,求实数
恒成立,求实数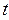 的取值范围.
的取值范围.
(12分)某商品定价为每件60元,不加收附加税时每年大约销售80万件,若政府征收附加税,每销售100元要征收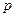 元(即税率为
元(即税率为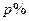 ),因此每年销量将减少
),因此每年销量将减少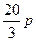 万件.
万件.
(1)将政府每年对该商品征收的总税金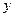 (万元),表示成
(万元),表示成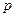 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域;
(2)要使政府在此项经营中每年收取的税金不少于128万元,问税率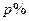 应怎样确定?
应怎样确定?